题目内容
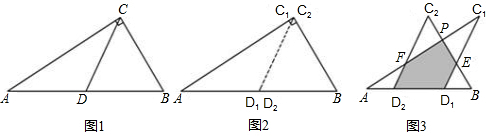
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6。沿斜边AB的中线CD把这张纸片剪成
 和
和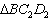 两个三角形(如图2所示)。将纸片
两个三角形(如图2所示)。将纸片 沿直线
沿直线 方向平移(点
方向平移(点 始终在同一直线上),当点
始终在同一直线上),当点 与点B重合时,停止平移。在平移的过程中,
与点B重合时,停止平移。在平移的过程中, 交于点E,
交于点E, 与
与 分别交于点F、P。
分别交于点F、P。
 和
和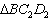 两个三角形(如图2所示)。将纸片
两个三角形(如图2所示)。将纸片 沿直线
沿直线 方向平移(点
方向平移(点 始终在同一直线上),当点
始终在同一直线上),当点 与点B重合时,停止平移。在平移的过程中,
与点B重合时,停止平移。在平移的过程中, 交于点E,
交于点E, 与
与 分别交于点F、P。
分别交于点F、P。
(1)当 平移到如图3所示位置时,猜想
平移到如图3所示位置时,猜想 与
与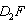 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2)设平移距离 为x,
为x,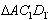 和
和 重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的 ?若存在,请求出x的值;若不存在,请说明理由。
?若存在,请求出x的值;若不存在,请说明理由。
 平移到如图3所示位置时,猜想
平移到如图3所示位置时,猜想 与
与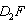 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;(2)设平移距离
 为x,
为x,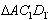 和
和 重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的
 ?若存在,请求出x的值;若不存在,请说明理由。
?若存在,请求出x的值;若不存在,请说明理由。 解:(1)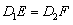 。
。
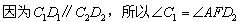 ,
,
又因为∠ACB=90°,CD是斜边上的中线,
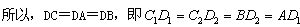 ,
,
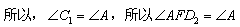 ,
,
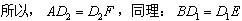 ,
,
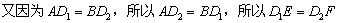 。
。
(2)因为在Rt△ABC中,AC=8,BC=6,
所以由勾股定理,得AB=10,
即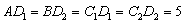 ,
,
又因为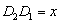 ,
,
所以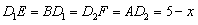 ,
,
所以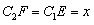 ,
,

 ,
,
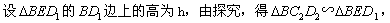
所以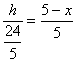 ,
,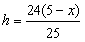 ,
,
所以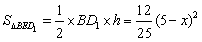 ,
,
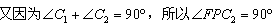 ,
,
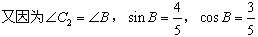 ,
,
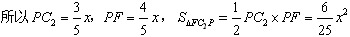 ,
,
而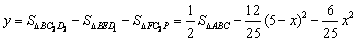 ,
,
所以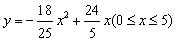 。
。
(3)存在,当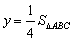 时,即
时,即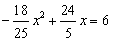 ,
,
整理,得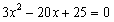 ,解得
,解得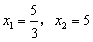 ,
,
 。
。
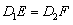 。
。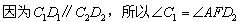 ,
,又因为∠ACB=90°,CD是斜边上的中线,
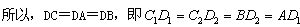 ,
,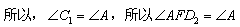 ,
,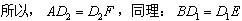 ,
,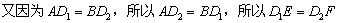 。
。(2)因为在Rt△ABC中,AC=8,BC=6,
所以由勾股定理,得AB=10,
即
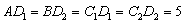 ,
,又因为
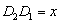 ,
,所以
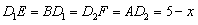 ,
,所以
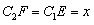 ,
,
 ,
,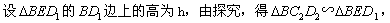
所以
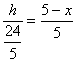 ,
,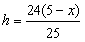 ,
,所以
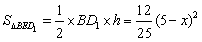 ,
,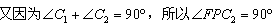 ,
,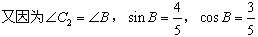 ,
,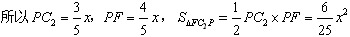 ,
,而
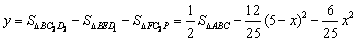 ,
,所以
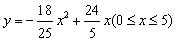 。
。(3)存在,当
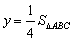 时,即
时,即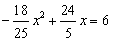 ,
,整理,得
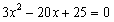 ,解得
,解得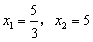 ,
, 。
。
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.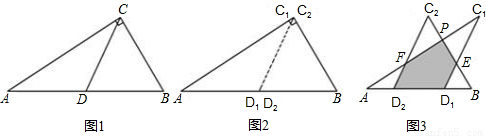
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.