题目内容
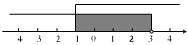
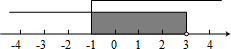 已知不等式组的解集用数轴表示如图所示:请写出满足解集的一个不等式组是
已知不等式组的解集用数轴表示如图所示:请写出满足解集的一个不等式组是
|
|
分析:由图示可看出,从-1出发向右画出的折线且表示-1的点是实心圆,表示x≥-1;从3出发向左画出的折线且表示3的点是空心圆,表示x<3,所以这个不等式组的解集为-1≤x<3,只要解集为-1≤x<3的不等式组皆可.
解答:解:根据图示知,该不等式组的解集是:-1≤x<3.
则
,即
符合题意.
故答案可以是:
.
则
|
|
故答案可以是:
|
点评:本题考查了不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某饮料厂为了开发新产品,用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制x千克,两种饮料的成本总额为y元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
每千克饮料 果汁含量 果汁 |
甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
某饮料厂为了开发新产品,用 种果汁原料和
种果汁原料和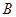 种果汁原料试制新型甲、乙两种饮料 共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料 共50千克,设甲种饮料需配制 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)若用19千克 种果汁原料和17.2千克
种果汁原料和17.2千克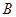 种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据:
种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据:
 每千克饮料 每千克饮料果汁含量 果汁 | 甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使 值最小,最小值是多少?
值最小,最小值是多少? 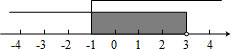 已知不等式组的解集用数轴表示如图所示:请写出满足解集的一个不等式组是________.
已知不等式组的解集用数轴表示如图所示:请写出满足解集的一个不等式组是________.