题目内容
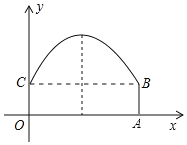
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 沿边
沿边![]() ,
,![]() 匀速运动到点
匀速运动到点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() ,
,![]() ,则能够反映
,则能够反映![]() 与
与![]() 之间函数关系的图象大致是( )
之间函数关系的图象大致是( )

A.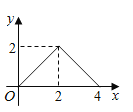 B.
B.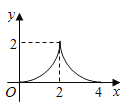 C.
C. D.
D.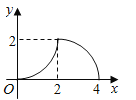
【答案】D
【解析】
分两种情况:①当P点在OA上时,即0≤x≤2时;②当P点在AB上时,即2<x≤4时,求出这两种情况下的PC长,则y=![]() PCOC的函数式可用x表示出来,对照选项即可判断.
PCOC的函数式可用x表示出来,对照选项即可判断.
解:∵△AOB是等腰直角三角形,AB=![]() ,
,
∴OB=4.
①当P点在OA上时,即0≤x≤2时,
PC=OC=x,S△POC=y=![]() PCOC=
PCOC=![]() x2,
x2,
是开口向上的抛物线,当x=2时,y=2;
OC=x,则BC=4-x,PC=BC=4-x,
S△POC=y=![]() PCOC=
PCOC=![]() x(4-x)=-
x(4-x)=-![]() x2+2x,
x2+2x,
是开口向下的抛物线,当x=4时,y=0.
综上所述,D答案符合运动过程中y与x的函数关系式.
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .