Question

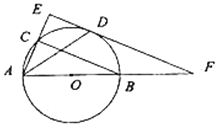
【题目】已知：如图，做的平分线，在的两边上分别截取，再以点为圆心，线段长为半径画弧，交于点，连接.

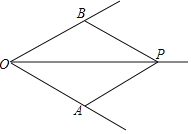
（1）求证：四边形是菱形；

（2）尺规作图：作线段的垂直平分线，分别交于点,于点，连接（不写做法，保留作图痕迹）；

（3）当时，判断的形状，并说明理由.

Answer 1

【答案】（1）见解析；（2）见解析；（3）△PBE是直角三角形，见解析.

【解析】

（1）根据四边相等的四边形是菱形即可证明．

（2）利用尺规周长线段OA的垂直平分线即可．

（3）结论：△PBE是直角三角形．想办法证明∠PBE=90°即可．

（1）证明：∵OP是∠AOB的平分线，

∴∠AOP=∠BOP，

∵OA=OB，OP=OP，

∴△AOP≌△BOP（SAS）

∴AP=BP，

∵OA=AP，

∴OA=OB=BP=AP，

∴四边形OAPB是菱形．

（2）解：如图所示．

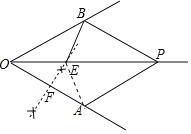
（3）解：结论：△PBE是直角三角形．

理由：连接AE，∵EF是线段OA的垂直平分线，

∴AE=OE，

∵PB=PA，∠EPB=∠EPA，PE=PE，

∴△AEP≌△BEP（SAS），

∴AE=BE，

∴OE=BE，

∴∠BOE=∠OBE，

当∠AOB=60°时，∠BOE=30°，

∴∠OBE=30°，

∵OB=BP，

∴∠BPO=∠BOE=30°，

∴∠OBP=180°-2∠BPO=180°-2×30°=120°，

∴∠PBE=∠OBP-∠OBE=120°-30°=90°，

∴△PBE是直角三角形．