题目内容
【题目】如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)△CDP与△PAE相似吗?如果相似,请写出证明过程;
(2)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.
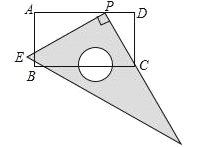
【答案】(1)△CDP∽△PAE;(2)DP=8.
【解析】试题分析:(1)由在矩形ABCD中,直角尺的直角顶点P在AD上滑动时,一直角边始终经过点C,另一直角边与AB交于点E,易得∠A=∠D=90°,∠APE=∠PCD,继而证得△CDP与△PAE相似;
(2)假设存在满足条件的点P,设DP=x,则AP=AD-DP=11-x,由相似三角形的周长比等于相似比,易得![]() =2,继而求得答案.
=2,继而求得答案.
试题解析:解:(1)△CDP∽△PAE.证明如下:
∵四边形ABCD是矩形,∴∠D=∠A=90°,CD=AB=6,∴∠PCD+CPD=90°.∵∠CPE=90°,∴∠APE+∠CPD=90°,∴∠APE=∠PCD,∴△CDP∽△PAE;
(2)假设存在满足条件的点P,设DP=x,则AP=AD﹣DP=11﹣x.∵△CDP∽△PAE,∴ ![]() =2,∴
=2,∴![]() =2,解得:x=8,∴AP=3,AE=4,即DP=8.
=2,解得:x=8,∴AP=3,AE=4,即DP=8.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目