��Ŀ����
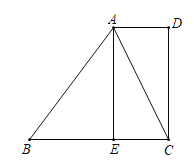
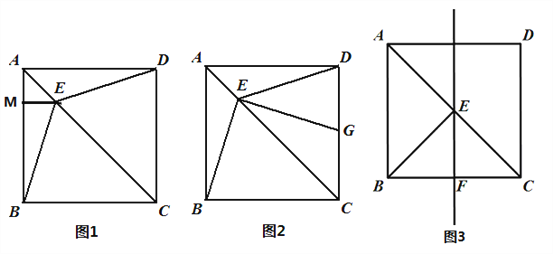
����Ŀ����ͼ����������ABCD�У�AB=4����E�ڶԽ���AC�ϣ�����BE��DE��
��1����ͼ1����EM��AB��AB�ڵ�M����AE=![]() ʱ����BE�ij���
ʱ����BE�ij���
��2����ͼ2����EG��BE��CD�ڵ�G����֤��BE=EG��
��3����ͼ3����EF��BC��BC�ڵ�F����BF=x����BEF�����Ϊy����xȡ��ֵʱ��yȡ�����ֵ�����ֵ�Ƕ��٣�����BEF�����ȡ�����ֵʱ����ֱ��EFȡ��P������BP��PC��ʹ�á�BPC=45������EP�ij�����
���𰸡�(1) ![]() (2)������(3)
(2)������(3) ![]()
�������������������1������E��EM��AB����AB�ڵ�M����AM=EM=1�����ɹ��ɶ������BE=![]() ��
��
��2����֤��BCE�ա�DCE����BE=DE������֤����EDG=��EGD����EG=ED���Ӷ��ó����ۣ�
��3�����������������ʽ�ú�����ϵʽ![]() ���Ӷ��ó�����.
���Ӷ��ó�����.
�����������1������E��EM��AB����AB�ڵ�M��
��AE=![]() ������AM=EM=1��
������AM=EM=1��
��BM=3��
��BE=![]()
��2����֤��BCE�ա�DCE��
�� BE=DE����CBE=��CDE
��EG��BE����BCD=90����
���CBE+��CGE=��CGE+��EGD=180��
���CBE=��EGD
���EDG=��EGD
��EG=ED
��EG=BE
��3��![]()
��![]() ʱ��
ʱ��
![]()
��ͼ��������á�EPC=��ECP=22.5����
��PE=CE=![]() ��
��
![]()


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�