题目内容
【题目】已知实数a,b,满足 ![]() =0,c是
=0,c是 ![]() 的整数部分,求a+2b+3c的平方根.
的整数部分,求a+2b+3c的平方根.
【答案】解:∵实数a,b,满足 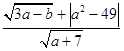 =0,
=0,
∴a2﹣49=0,
∴a=±7,
∵a+7>0,
∴a=7,
∵3a﹣b=0,
∴b=21,
∵c是 ![]() 的整数部分,
的整数部分,
∴c=5,
∴a+2b+3c=7+2×21+3×5=64,
∴a+2b+3c的平方根为±8
【解析】根据分式和二次根式、绝对值有意义的条件求出a的值,再根据3a﹣b=0,求出b的值,根据c是 ![]() 的整数部分,求出c的值,把它们的值代入要求的式子,然后求求出平方根即可.
的整数部分,求出c的值,把它们的值代入要求的式子,然后求求出平方根即可.
【考点精析】解答此题的关键在于理解平方根的基础的相关知识,掌握如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟);一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目