题目内容
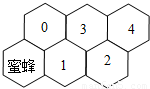
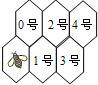 8、假定有一排蜂房,形状如图,一只蜜蜂在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,密封爬到1号蜂房的爬法有:蜜蜂?1号;蜜蜂?0号?1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法( )
8、假定有一排蜂房,形状如图,一只蜜蜂在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,密封爬到1号蜂房的爬法有:蜜蜂?1号;蜜蜂?0号?1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法( )分析:本题可分两种情况进行讨论:①蜜蜂先向右爬行;②蜜蜂先向右上爬行;两种情况.可分别求出两种情况的不同爬法,进而可得出一共有多少种不同的爬法.
解答:解:本题分两种情况:
①蜜蜂先向右爬行;则有:
一、1号?3号?4号;二、1号?2号?4号;三、1号?2号?3号?4号;
共3种爬法;
②蜜蜂先向右上爬行;则有:
一、0号?2号?4号;二、0号?1号?2号?4号;三、0号?1号?3号?4号;
四、0号?1号?2号?3号?4号;五、0号?2号?3号?4号;
共5种爬法;
因此蜜蜂从最初位置爬到4号蜂房共有3+5=8种不同的爬法.故选B.
①蜜蜂先向右爬行;则有:
一、1号?3号?4号;二、1号?2号?4号;三、1号?2号?3号?4号;
共3种爬法;
②蜜蜂先向右上爬行;则有:
一、0号?2号?4号;二、0号?1号?2号?4号;三、0号?1号?3号?4号;
四、0号?1号?2号?3号?4号;五、0号?2号?3号?4号;
共5种爬法;
因此蜜蜂从最初位置爬到4号蜂房共有3+5=8种不同的爬法.故选B.
点评:解决问题的关键是读懂题意,注意蜂房的排列顺序以及蜜蜂爬行的规则要求.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 15、假定有一排蜂房,形状如图,一只蜜峰在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号共有2种不同的爬法,若蜜蜂从最初位置爬到4号蜂房共有n种不同爬法,则n等于
15、假定有一排蜂房,形状如图,一只蜜峰在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号共有2种不同的爬法,若蜜蜂从最初位置爬到4号蜂房共有n种不同爬法,则n等于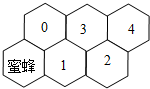 10、假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去.则从最初位置爬到4号蜂房中,不同的爬法有( )
10、假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去.则从最初位置爬到4号蜂房中,不同的爬法有( )