题目内容
【题目】抛物线y=﹣x2+2x+3与x轴交于点A，B（A在B的左侧），与y轴交于点C．
（1）求直线BC的解析式；
（2）抛物线的对称轴上存在点P，使∠APB=∠ABC，利用图1求点P的坐标；
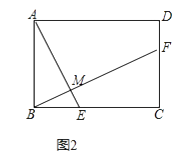
（3）点Q在y轴右侧的抛物线上，利用图2比较∠OCQ与∠OCA的大小，并说明理由．
【答案】
（1）
解：在y=﹣x2+2x+3中，令y=0可得0=﹣x2+2x+3，解得x=﹣1或x=3，令x=0可得y=3，
∴B（3，0），C（0，3），
∴可设直线BC的解析式为y=kx+3，
把B点坐标代入可得3k+3=0，解得k=﹣1，
∴直线BC解析式为y=﹣x+3；
（2）
解：∵OB=OC，
∴∠ABC=45°，
∵y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴抛物线对称轴为x=1，
设抛物线对称轴交直线BC于点D，交x轴于点E，当点P在x轴上方时，如图1，
∵∠APB=∠ABC=45°，且PA=PB，
∴∠PBA= 
=67.5°，∠DPB= 
∠APB=22.5°，
∴∠PBD=67.5°﹣45°=22.5°，
∴∠DPB=∠DBP，
∴DP=DB，
在Rt△BDE中，BE=DE=2，由勾股定理可求得BD=2 
，
∴PE=2+2 ，
∴P（1，2+2 ）；
当点P在x轴下方时，由对称性可知P点坐标为（1，﹣2﹣2 ）；
综上可知P点坐标为（1，2+2 ）或（1，﹣2﹣2 ）；
（3）
解：设Q（x，﹣x2+2x+3），当点Q在x轴下方时，如图2，过Q作QF⊥y轴于点F，
当∠OCA=∠OCQ时，则△QEC∽△AOC，
∴ 
= 
= 
，即 
= ，解得x=0（舍去）或x=5，
∴当Q点横坐标为5时，∠OCA=∠OCQ；
当Q点横坐标大于5时，则∠OCQ逐渐变小，故∠OCA＞∠OCQ；
当Q点横坐标小于5且大于0时，则∠OCQ逐渐变大，故∠OCA＜∠OCQ．
【解析】（1）由抛物线解析式可求得B、C的坐标，利用待定系数法可求得直线BC的解析式；（2）由直线BC解析式可知∠APB=∠ABC=45°，设抛物线对称轴交直线BC于点D，交x轴于点E，结合二次函数的对称性可求得PD=BD，在Rt△BDE中可求得BD，则可求得PE的长，可求得P点坐标；（3）设Q（x，﹣x2+2x+3），当∠OCQ=∠OCA时，利用两角的正切值相等可得到关于x的方程，可求得Q点的横坐标，再结合图形可比较两角的大小．
【考点精析】认真审题，首先需要了解确定一次函数的表达式(确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法)，还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键．
