题目内容
 (1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )
(1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )分析:首先连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,易求得O1D的长,利用三角函数的知识求得∠O2的度数,继而可求得梯形与扇形的面积,则可求得答案.
解答: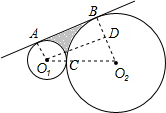 解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
∵⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,⊙O1的半径为1,⊙O2的半径为3,
∴四边形AO1DB是矩形,
∴O1A=BD,
∴O1A=1,O2B=3,O1O2=1+3=4,
∴O2D=3-1=2,
∴O1D=
=2
,
∴tan∠O2=
=
,
∴∠O2=60°,
∴∠AO1O2=180°-∠O2=120°,
∴S梯形ABO2O1=
(O1A+O2B)•O1D=
×(1+3)×2
=4
,S扇形AO1C=
×π×12=
π,S扇形BO2C=
×π×32=
π,
∴S阴影=S梯形ABO2O1-S扇形AO1C-S扇形BO2C=4
-
π.
故选B.
 解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,∵⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,⊙O1的半径为1,⊙O2的半径为3,
∴四边形AO1DB是矩形,
∴O1A=BD,
∴O1A=1,O2B=3,O1O2=1+3=4,
∴O2D=3-1=2,
∴O1D=
| O1O22-O2D2 |
| 3 |
∴tan∠O2=
| O1D |
| O2D |
| 3 |
∴∠O2=60°,
∴∠AO1O2=180°-∠O2=120°,
∴S梯形ABO2O1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 120 |
| 360 |
| 1 |
| 3 |
| 60 |
| 360 |
| 3 |
| 2 |
∴S阴影=S梯形ABO2O1-S扇形AO1C-S扇形BO2C=4
| 3 |
| 11 |
| 6 |
故选B.
点评:此题考查了相切两圆的性质、梯形的性质、勾股定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
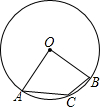 (1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )
(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( ) (1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( )
(1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( ) (1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )
(1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )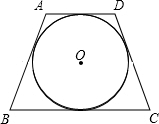 (1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为
(1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为 (1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=
(1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=