题目内容
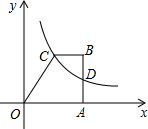 (2013•许昌一模)如图,双曲线y=
(2013•许昌一模)如图,双曲线y=| k |
| x |
| 3 |
| 3 |
分析:设C点坐标为(a,b),根据∠AOC=60°,可以用a表示出b,再利用D是AB的中点,OA=2,求出D点坐标,把C点和D点坐标代入双曲线解析式,求出a的值,进而求出k的值.
解答:解:设C点坐标为(a,b),
∵∠AOC=60°,
∴b=
a,
∵四边形OABC是直角梯形,
∴点B和点C的纵坐标相同,
∴C点的纵坐标为
a,
∵D是AB的中点,OA=2,
∴D(2,
),
∵点D和点C都在双曲线y=
上,
∴
a2=
a,
解得a=1,
∴C点坐标为(1,
),
∵点C都在双曲线y=
上,
∴k=
,
故答案为
.
∵∠AOC=60°,
∴b=
| 3 |
∵四边形OABC是直角梯形,
∴点B和点C的纵坐标相同,
∴C点的纵坐标为
| 3 |
∵D是AB的中点,OA=2,
∴D(2,
| ||
| 2 |
∵点D和点C都在双曲线y=
| k |
| x |
∴
| 3 |
| 3 |
解得a=1,
∴C点坐标为(1,
| 3 |
∵点C都在双曲线y=
| k |
| x |
∴k=
| 3 |
故答案为
| 3 |
点评:本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握反比例函数图象上的每一个点的纵横坐标之积是常数k,此题难度不大.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目

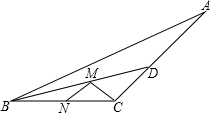 (2013•许昌一模)如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为
(2013•许昌一模)如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为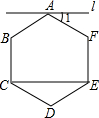 (2013•许昌一模)如图,CE是正六边形ABCDEF的一条对角线,过顶点A作直线l∥CE,则∠1的度数为
(2013•许昌一模)如图,CE是正六边形ABCDEF的一条对角线,过顶点A作直线l∥CE,则∠1的度数为