Question

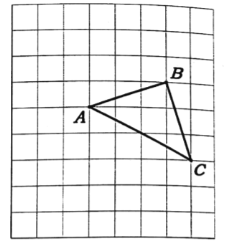
【题目】如图，在边长为1的正方形组成的网格中，的顶点均在格点上，绕点顺时针旋转后得到.

（1）画出；（其中、对应点分别是、）

（2）分别画出旋转过程中，点点经过的路径；

①求点经过的路径的长；

②求线段所扫过的面积.

Answer 1

【答案】(1)作图见详解;(2)作图见详解;①;②.

【解析】

(1)根据旋转的性质作出图形即可;

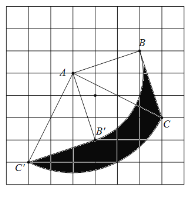
(2)根据对应点到旋转中心的距离相等可知点B点C经过的路径分别为以A圆心,AB,AC为半径的圆弧;①根据题意求出劣弧BB’的长即可;②如图,BC边扫过的面积为阴影部分的面积,它等于扇形ACC’的面积+△ABC的面积-扇形ABB’的面积-△AB’C’的面积,根据旋转的性质可知△ABC的面积=△AB’C’的面积,故阴影部分的面积=扇形ACC’的面积-扇形ABB’的面积即可.

解:(1)如图所示:

(2)如图所示:

①AB==,

∴弧BB’的长==.

②∵AC===2,

∴线段所扫过的面积=扇形ACC’的面积+△ABC的面积-扇形ABB’的面积-△AB’C’的面积

∵△ABC的面积=△AB’C’的面积,

∴线段所扫过的面积=扇形ACC’的面积-扇形ABB’的面积

=-

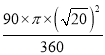=5-

=.