题目内容
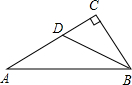（2012•绵阳）已知△ABC中，∠C=90°，tanA=| 1 |
| 2 |
分析：作DE⊥AB于点E，根据相等的角的三角函数值相等即可得到
=
=
=
，设CD=1，则可以求得AD的长，然后利用勾股定理即可求得DE、AE的长，则BE可以求得，根据同角三角函数之间的关系即可求解．
| BC |
| AC |
| CD |
| BC |
| DE |
| AE |
| 1 |
| 2 |
解答：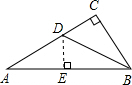
解：作DE⊥AB于点E．
∵∠CBD=∠A，
∴tanA=tan∠CBD=
=
=
=
，
设CD=1，则BC=2，AC=4，
∴AD=AC-CD=3，
在直角△ABC中，AB=
=
=2
，
在直角△ADE中，设DE=x，则AE=2x，
∵AE2+DE2=AD2，
∴x2+（2x）2=9，
解得：x=
，
则DE=
，AE=
．
∴BE=AB-AE=2
-
=
，
∴tan∠DBA=
=
，
∴sin∠DBA=
．
故选A．
解：作DE⊥AB于点E．∵∠CBD=∠A，
∴tanA=tan∠CBD=
| BC |
| AC |
| CD |
| BC |
| DE |
| AE |
| 1 |
| 2 |
设CD=1，则BC=2，AC=4，
∴AD=AC-CD=3，
在直角△ABC中，AB=
| AC2+BC2 |
| 4+16 |
| 5 |
在直角△ADE中，设DE=x，则AE=2x，
∵AE2+DE2=AD2，
∴x2+（2x）2=9，
解得：x=
3
| ||
| 5 |
则DE=
3
| ||
| 5 |
6
| ||
| 5 |
∴BE=AB-AE=2
| 5 |
6
| ||
| 5 |
4
| ||
| 5 |
∴tan∠DBA=
| DE |
| BE |
| 3 |
| 4 |
∴sin∠DBA=
| 3 |
| 5 |
故选A．
点评：本题考查了三角函数的定义，以及勾股定理，正确理解三角函数就是直角三角形中边的比值是关键．
练习册系列答案
相关题目
