题目内容
如图,在平面直角坐标系xOy中,点A( ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.

 ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.

(1)①作图见解析;②(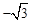 ,1);(2)当
,1);(2)当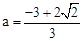 时,公共点在第三象限, 当
时,公共点在第三象限, 当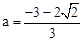 时,公共点在第二象限.
时,公共点在第二象限.
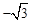 ,1);(2)当
,1);(2)当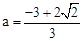 时,公共点在第三象限, 当
时,公共点在第三象限, 当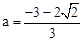 时,公共点在第二象限.
时,公共点在第二象限.试题分析:(1)①根据轴对称的性质,作点C关于直线AB的对称点D,连接OD,OD与直线AB的交点P 即为所求.
②应用待定系数法求出直线AB和直线OD的表达式,联立二者即为所求.
(2)根据抛物线y=ax2+bx+c经过点O、C,得出解析式为
 ,根据抛物线
,根据抛物线 与直线
与直线 只有一个公共点得到
只有一个公共点得到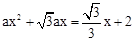 的根的差别式等于0,从而求得a的值,进而求得交点坐标,判断出其所在象限.
的根的差别式等于0,从而求得a的值,进而求得交点坐标,判断出其所在象限.(1)①如图1.
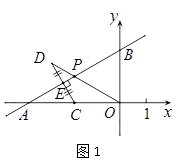
②如图2,作DF⊥OA于点F,根据题意,得AC=CO=
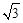 ,∠BAO=30°,CE=DE,
,∠BAO=30°,CE=DE,∴ CD=
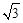 ,CF=
,CF=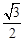 ,DF=
,DF= .∴ D(
.∴ D( ,
, ).
).求得直线AB的表达式为
 ,直线OD的表达式为
,直线OD的表达式为 ,
,∴ P(
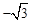 ,1).
,1).在△DFO中,可求得 DO=3.∴PC+PO的最小值为3.

(2)∵抛物线y=ax2+bx+c经过点O、C,
∴
 .
.由题意,得
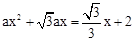 .
. 整理,得
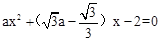 .
.∵
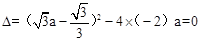 .∴
.∴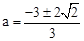 .
.当
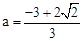 时,公共点在第三象限, 当
时,公共点在第三象限, 当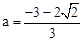 时,公共点在第二象限.
时,公共点在第二象限.
练习册系列答案
相关题目
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .其中,是一次函数的有( )
.其中,是一次函数的有( ) x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
 ,连结
,连结 、
、 .若∠ACB=30°,AB=2,
.若∠ACB=30°,AB=2, =x,四边形
=x,四边形 的面积为S.
的面积为S. ,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).

