题目内容
(本题满分10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
解:(1)∵
|
| 1 | 2 | 3 |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)=![]() =
=![]() .
.
(3)∵
|
| 1 | 2 | 3 |
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
∴P(点M的横坐标与纵坐标之和是偶数)=![]() .
.
解析:略

练习册系列答案
相关题目
 次后在函数 的图象上.(请填写相应的解析式)
次后在函数 的图象上.(请填写相应的解析式)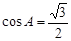 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长. ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长. 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.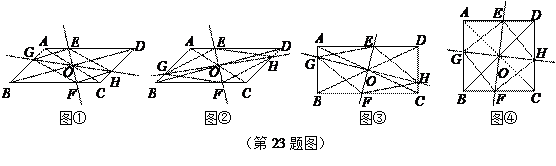
 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长.