ΧβΡΩΡΎ»ί
ΫώΡξΡœΖΫΡ≥ΒΊΖΔ…ζΒΊ’πΘ§’ΰΗ°ΈΣΝΥΨΓΩλ¥νΫ®ΑεΖΩΑ≤÷Ο‘÷ΟώΘ§ΗχΡ≥≥ßœ¬¥οΝΥ…ζ≤ζA÷÷Αε≤Ρ48000 ΚΆB÷÷Αε≤Ρ24000
ΚΆB÷÷Αε≤Ρ24000 »ΈΈώ.
»ΈΈώ.
Δ≈»γΙϊΗΟ≥ßΑ≤≈≈210»Υ…ζ≤ζ’βΝΫ÷÷≤ΡΘ§ΟΩ»ΥΟΩΧλΡή…ζ≤ζA÷÷Αε≤Ρ60 ΜρB÷÷Αε≤Ρ
ΜρB÷÷Αε≤Ρ
40 Θ§«κΈ ΘΚ”ΠΖ÷±πΑ≤≈≈Εύ…Ό»Υ…ζ≤ζA÷÷Αε≤ΡΚΆB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώΘΩ
Θ§«κΈ ΘΚ”ΠΖ÷±πΑ≤≈≈Εύ…Ό»Υ…ζ≤ζA÷÷Αε≤ΡΚΆB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώΘΩ
ΔΤΡ≥‘÷ΟώΑ≤÷ΟΒψΦΤΜ°”ΟΗΟ≥ß…œ ωœ¬¥ο»ΈΈώ…ζ≤ζΒΡΝΫ÷÷Αε≤Ρ¥νΫ®ΦΉΓΔ““ΝΫ÷÷ΙφΗώΒΡΑεΖΩ
Ι≤400ΦδΘ§“―÷ΣΫ®…η“ΜΦδΦΉ–ΆΑεΖΩΚΆ“ΜΦδ““–ΆΑεΖΩΥυ–ηΑε≤ΡΦΑΑ≤÷Ο»Υ ΐ»γœ¬±μΥυ ΨΘΚ
Έ ΘΚ’β400ΦδΑεΖΩΒΡ¥νΫ®Ι≤”–Εύ…Ό÷÷ΖΫΑΗΘΩ’β–©ΖΫΑΗ÷–ΡήΉνΕύΒΊΑ≤÷Ο‘÷ΟώΒΡ «ΡΡ“Μ÷÷ΘΩΉνΕύΡήΑ≤÷Ο‘÷ΟώΕύ…Ό»ΥΘΩ
 ΚΆB÷÷Αε≤Ρ24000
ΚΆB÷÷Αε≤Ρ24000 »ΈΈώ.
»ΈΈώ.Δ≈»γΙϊΗΟ≥ßΑ≤≈≈210»Υ…ζ≤ζ’βΝΫ÷÷≤ΡΘ§ΟΩ»ΥΟΩΧλΡή…ζ≤ζA÷÷Αε≤Ρ60
 ΜρB÷÷Αε≤Ρ
ΜρB÷÷Αε≤Ρ40
 Θ§«κΈ ΘΚ”ΠΖ÷±πΑ≤≈≈Εύ…Ό»Υ…ζ≤ζA÷÷Αε≤ΡΚΆB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώΘΩ
Θ§«κΈ ΘΚ”ΠΖ÷±πΑ≤≈≈Εύ…Ό»Υ…ζ≤ζA÷÷Αε≤ΡΚΆB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώΘΩΔΤΡ≥‘÷ΟώΑ≤÷ΟΒψΦΤΜ°”ΟΗΟ≥ß…œ ωœ¬¥ο»ΈΈώ…ζ≤ζΒΡΝΫ÷÷Αε≤Ρ¥νΫ®ΦΉΓΔ““ΝΫ÷÷ΙφΗώΒΡΑεΖΩ
Ι≤400ΦδΘ§“―÷ΣΫ®…η“ΜΦδΦΉ–ΆΑεΖΩΚΆ“ΜΦδ““–ΆΑεΖΩΥυ–ηΑε≤ΡΦΑΑ≤÷Ο»Υ ΐ»γœ¬±μΥυ ΨΘΚ
| ΑεΖΩ | A÷÷Αε≤ΡΘ® Θ© Θ© | B÷÷Αε≤ΡΘ® Θ© Θ© | Α≤÷Ο»Υ ΐ |
| ΦΉ–Ά | 108 | 61 | 12 |
| ““–Ά | 156 | 51 | 10 |
Θ®1Θ©Α≤≈≈120»Υ…ζ≤ζA÷÷Αε≤ΡΘ§90»Υ…ζ≤ζB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώΘ®2Θ©¥νΫ®ΖΫΑΗΙ≤”–61÷÷ΘΜ¥νΫ®ΦΉ–Ά360ΦδΘ§““–Ά40Φδ ±Θ§ΡήΑ≤÷ΟΉνΕύΒΡ‘÷Οώ
4720»Υ
4720»Υ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©…η
 »Υ…ζ≤ζA÷÷Αε≤ΡΘ§ΗυΨίΧβ“βΒΟΘΚ
»Υ…ζ≤ζA÷÷Αε≤ΡΘ§ΗυΨίΧβ“βΒΟΘΚ Θ§ΫβΒΟΘ§
Θ§ΫβΒΟΘ§ =120
=120Ψ≠Φλ―ι
 =120 «Ζ÷ ΫΖΫ≥ΧΒΡΫβ
=120 «Ζ÷ ΫΖΫ≥ΧΒΡΫβ Γύ210©¹120=90Θ§
¥πΘΚΑ≤≈≈120»Υ…ζ≤ζA÷÷Αε≤ΡΘ§90»Υ…ζ≤ζB÷÷Αε≤ΡΘ§≤≈Ρή»Ζ±ΘΆ§ ±Άξ≥…ΗςΉ‘ΒΡ…ζ≤ζ»ΈΈώ
Θ®2Θ©…η¥νΫ®ΦΉ÷÷ΑεΖΩ
 ΦδΘ§‘ρ¥νΫ®““÷÷ΑεΖΩΈΣΘΚ400-
ΦδΘ§‘ρ¥νΫ®““÷÷ΑεΖΩΈΣΘΚ400- ΦδΘ§ΡήΑ≤÷Ο»Υ ΐΈΣM»Υ.
ΦδΘ§ΡήΑ≤÷Ο»Υ ΐΈΣM»Υ.“άΧβ“β”–
 Ϋβ’βΗω≤ΜΒ» ΫΉιΒΟΘΚ300Γή
Ϋβ’βΗω≤ΜΒ» ΫΉιΒΟΘΚ300Γή Γή360
Γή360ΓΏ
 ΈΣ’ϊ ΐΘ§Γύ¥νΫ®ΖΫΑΗΙ≤”–61÷÷
ΈΣ’ϊ ΐΘ§Γύ¥νΫ®ΖΫΑΗΙ≤”–61÷÷ ΓύΗυΨίΧβ“βΘ§Α≤÷Ο»Υ ΐM=12
 +10Θ®400©¹
+10Θ®400©¹ Θ©=2
Θ©=2 +4000 Θ®300Γή
+4000 Θ®300Γή Γή360Θ©
Γή360Θ©ΓΏ2ΘΨ0Θ§Γύ M =2
 +4000 Υφ
+4000 Υφ ‘ω¥σΕχ‘ω¥σΘ§ΓύΒ±
‘ω¥σΕχ‘ω¥σΘ§ΓύΒ± =360 ±Α≤÷ΟΒΡ»Υ ΐΉνΕύΘ§Γύ400-360=40Θ§
=360 ±Α≤÷ΟΒΡ»Υ ΐΉνΕύΘ§Γύ400-360=40Θ§Γύ¥νΫ®ΦΉ–Ά360ΦδΘ§““–Ά40Φδ ±Θ§ΡήΑ≤÷ΟΉνΕύΒΡ‘÷Οώ

¥πΘΚ¥νΫ®ΦΉ–Ά360ΦδΘ§““–Ά40Φδ ±Θ§ΡήΑ≤÷ΟΉνΕύΒΡ‘÷Οώ4720»Υ
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΖ÷ ΫΖΫ≥ΧΘ§Ϋβ¥π±ΨΧβΒΡ÷ΊΒψ «Ν–≥ωΖ÷ ΫΖΫ≥ΧΘ§Τδ¥Έ «’ΤΈ’Ζ÷ ΫΖΫ≥ΧΒΡΫβΖ®Θ§Μα«σΫβΖ÷ ΫΖΫ≥Χ

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
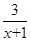 Θ≠
Θ≠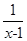 ΘΫ0Θ°
ΘΫ0Θ° Θ§≤ΔΑ―ΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥ΘΜ
Θ§≤ΔΑ―ΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥ΘΜ
 Θ°
Θ°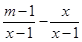 =0”–‘ωΗυΘ§‘ρmΒΡ÷Β «
=0”–‘ωΗυΘ§‘ρmΒΡ÷Β «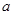 Θ§«σΙΊ”Ύ
Θ§«σΙΊ”Ύ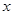 ΒΡΖ÷ ΫΖΫ≥Χ
ΒΡΖ÷ ΫΖΫ≥Χ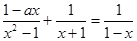 ΒΡΫβΘ§≤Δ«σΗΟΖΫ≥ΧΒΡΫβ≤Μ–Γ”Ύ
ΒΡΫβΘ§≤Δ«σΗΟΖΫ≥ΧΒΡΫβ≤Μ–Γ”Ύ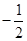 ΒΡΗ≈¬ Θ°
ΒΡΗ≈¬ Θ°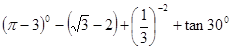 ΘΜ
ΘΜ 
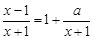 ÷–ΒΡa»Γœ¬Ν–Ρ≥Ηω÷Β ±Θ§ΗΟΖΫ≥Χ”–ΫβΘ§‘ρ’βΗωa «Θ® Θ©
÷–ΒΡa»Γœ¬Ν–Ρ≥Ηω÷Β ±Θ§ΗΟΖΫ≥Χ”–ΫβΘ§‘ρ’βΗωa «Θ® Θ©