题目内容
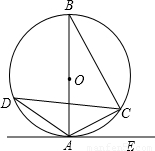
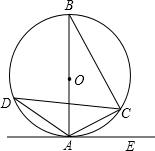 如图,已知△ABC外接⊙O,AB是⊙O的直径,AC=6cm,BC=8cm,且∠EAC=∠ADC.
如图,已知△ABC外接⊙O,AB是⊙O的直径,AC=6cm,BC=8cm,且∠EAC=∠ADC.(1)求⊙O的半径;
(2)求证:AE是⊙O的切线.
分析:(1)根据圆周角定理证得△ABC是直角三角形,在直角三角形中利用勾股定理即可求得直径AB的长度,继而求得该圆的半径的长度;
(2)欲证AE是⊙O的切线,直需证得AE⊥AB即可.
(2)欲证AE是⊙O的切线,直需证得AE⊥AB即可.
解答: (1)解:∵AB是⊙O的直径,
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
又∵AC=6cm,BC=8cm,
∴AB=10cm(勾股定理),
∴⊙O的半径=
AB=5cm;
(2)证明:由(1)知,∠ACB=90°,则∠ABC+∠BAC=90°(直角三角形的两个锐角互余);
∵∠ADC=∠ABC(同弧所对的圆周角相等),∠EAC=∠ADC(已知),
∴∠BAE=∠CAE+∠BAC=90°(等量代换),即AB⊥AE;
∵点A在⊙O上,
∴AE是⊙O的切线.
 (1)解:∵AB是⊙O的直径,
(1)解:∵AB是⊙O的直径,∴∠ACB=90°(直径所对的圆周角是直角),
又∵AC=6cm,BC=8cm,
∴AB=10cm(勾股定理),
∴⊙O的半径=
| 1 |
| 2 |
(2)证明:由(1)知,∠ACB=90°,则∠ABC+∠BAC=90°(直角三角形的两个锐角互余);
∵∠ADC=∠ABC(同弧所对的圆周角相等),∠EAC=∠ADC(已知),
∴∠BAE=∠CAE+∠BAC=90°(等量代换),即AB⊥AE;
∵点A在⊙O上,
∴AE是⊙O的切线.
点评:本题考查了圆周角定理、切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
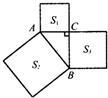 10、如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=81,S2=225,则S3=
10、如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=81,S2=225,则S3=
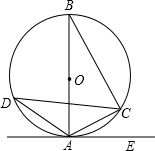 如图,已知△ABC外接⊙O,AB是⊙O的直径,AC=6cm,BC=8cm,且∠EAC=∠ADC.
如图,已知△ABC外接⊙O,AB是⊙O的直径,AC=6cm,BC=8cm,且∠EAC=∠ADC.