Question

（2008•上海）在△ABC中，AB=AC=5，cosB=

3

5

（如图）．如果圆O的半径为

10

，且经过点B，C，那么线段AO的长等于

3或5

．

Answer 1

分析：分两种情况考虑：（i）如图1所示，由AB=AC，OB=OC，利用线段垂直平分线逆定理得到AO垂直平分BC，在直角三角形ABD中，由AB及cos∠ABC的值，利用锐角三角函数定义求出BD的长，再利用勾股定理求出AD的长，在直角三角形OBD中，由OB与BD的长，利用勾股定理求出OD的长，由AD+DO即可求出AO的长；（ii）同理由AD-OD即可求出AO的长，综上，得到所有满足题意的AO的长．

解答：解：分两种情况考虑：

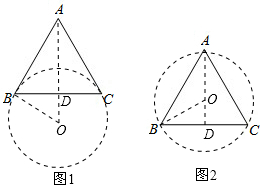
（i）如图1所示，
∵AB=AC，OB=OC，
∴AO垂直平分BC，
∴OA⊥BC，D为BC的中点，
在Rt△ABD中，AB=5，cos∠ABC=

3

5

，
∴BD=3，
根据勾股定理得：AD=

AB2-BD2

=4，
在Rt△BDO中，OB=

10

，BD=3，
根据勾股定理得：OD=

OB2-BD2

=1，
则AO=AD+OD=4+1=5；
（ii）如图2所示，
∵AB=AC，OB=OC，
∴AO垂直平分BC，
∴OD⊥BC，D为BC的中点，
在Rt△ABD中，AB=5，cos∠ABC=

3

5

，
∴BD=3，
根据勾股定理得：AD=

AB2-BD2

=4，
在Rt△BDO中，OB=

10

，BD=3，
根据勾股定理得：OD=

OB2-BD2

=1，
则OA=AD-OD=4-1=3，
综上，OA的长为3或5．
故答案为：3或5

点评：此题考查了垂径定理，勾股定理，等腰三角形的性质，以及直角三角形的性质，熟练掌握定理及性质是解本题的关键．