题目内容
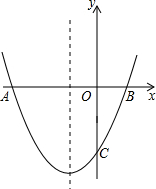 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0),C(0,-2)
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0),C(0,-2)(1)求这条抛物线的函数表达式;
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标;
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
分析:(1)已知抛物线过C(0,-2)点,那么c=-2;根据对称轴为x=-1,因此-
=-1,然后将A点的坐标代入抛物线中,通过联立方程组即可得出抛物线的解析式.
(2)本题的关键是确定P点的位置,由于A是B点关于抛物线对称轴的对称点,因此连接AC与抛物线对称轴的交点就是P点.可根据A,C的坐标求出AC所在直线的解析式,然后根据得出的一次函数的解析式求出与抛物线对称轴的交点即可得出P点的坐标.
(3)△PDE的面积=△OAC的面积-△PDC的面积-△ODE的面积-△AEP的面积
△OAC中,已知了A,C的坐标,可求出△OAC的面积.
△PDC中,以CD为底边,P的横坐标的绝对值为高,即可表示出△PDC的面积.
△ODE中,可先用m表示出OD的长,然后根据△ODE与△OAC相似,求出OE的长,根据三角形的面积计算公式可用m表示出△ODE的面积.
△PEA中,以AE为底边(可用OE的长表示出AE),P点的纵坐标的绝对值为高,可表示出△PEA的面积.
由此可表示出△ODE的面积,即可得出关于S,m的函数关系式.然后根据函数的性质求出三角形的最大面积以及对应的m的值.
| b |
| 2a |
(2)本题的关键是确定P点的位置,由于A是B点关于抛物线对称轴的对称点,因此连接AC与抛物线对称轴的交点就是P点.可根据A,C的坐标求出AC所在直线的解析式,然后根据得出的一次函数的解析式求出与抛物线对称轴的交点即可得出P点的坐标.
(3)△PDE的面积=△OAC的面积-△PDC的面积-△ODE的面积-△AEP的面积
△OAC中,已知了A,C的坐标,可求出△OAC的面积.
△PDC中,以CD为底边,P的横坐标的绝对值为高,即可表示出△PDC的面积.
△ODE中,可先用m表示出OD的长,然后根据△ODE与△OAC相似,求出OE的长,根据三角形的面积计算公式可用m表示出△ODE的面积.
△PEA中,以AE为底边(可用OE的长表示出AE),P点的纵坐标的绝对值为高,可表示出△PEA的面积.
由此可表示出△ODE的面积,即可得出关于S,m的函数关系式.然后根据函数的性质求出三角形的最大面积以及对应的m的值.
解答:解:(1)由题意得
,
解得
,
∴此抛物线的解析式为y=
x2+
x-2.
(2)连接AC、BC.
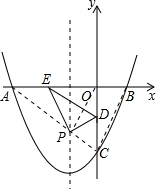
因为BC的长度一定,
所以△PBC周长最小,就是使PC+PB最小.
B点关于对称轴的对称点是A点,AC与对称轴x=-1的交点即为所求的点P.
设直线AC的表达式为y=kx+b,
则
,
解得
,
∴此直线的表达式为y=-
x-2,
把x=-1代入得y=-
∴P点的坐标为(-1,-
).
(3)S存在最大值,
理由:∵DE∥PC,即DE∥AC.
∴△OED∽△OAC.
∴
=
,即
=
,
∴OE=3-
m,OA=3,AE=
m,
∴S=S△OAC-S△OED-S△AEP-S△PCD
=
×3×2-
×(3-
m)×(2-m)-
×
m×
-
×m×1
=-
m2+
m=-
(m-1)2+
∵-
<0
∴当m=1时,S最大=
.
|
解得
|
∴此抛物线的解析式为y=
| 2 |
| 3 |
| 4 |
| 3 |
(2)连接AC、BC.

因为BC的长度一定,
所以△PBC周长最小,就是使PC+PB最小.
B点关于对称轴的对称点是A点,AC与对称轴x=-1的交点即为所求的点P.
设直线AC的表达式为y=kx+b,
则
|
解得
|
∴此直线的表达式为y=-
| 2 |
| 3 |
把x=-1代入得y=-
| 4 |
| 3 |
∴P点的坐标为(-1,-
| 4 |
| 3 |
(3)S存在最大值,
理由:∵DE∥PC,即DE∥AC.
∴△OED∽△OAC.
∴
| OD |
| OC |
| OE |
| OA |
| 2-m |
| 2 |
| OE |
| 3 |
∴OE=3-
| 3 |
| 2 |
| 3 |
| 2 |
∴S=S△OAC-S△OED-S△AEP-S△PCD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
=-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∵-
| 3 |
| 4 |
∴当m=1时,S最大=
| 3 |
| 4 |
点评:本题着重考查了待定系数法求二次函数解析式、三角形相似等重要知识点;
(3)中无法直接求出三角形的面积时,可用其他图形的面积经过“和,差”的关系来求出其面积.
(3)中无法直接求出三角形的面积时,可用其他图形的面积经过“和,差”的关系来求出其面积.

练习册系列答案
相关题目
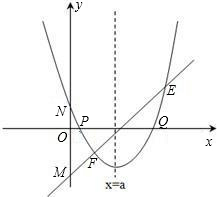 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.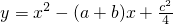 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.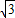 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.