题目内容
已知:AB∥CD,如图①,利用平行线的性质和三角形内角和定理可得:∠BAE+∠E+∠ECD=360°.
如图②,同样:∠BAE1+∠AE1E2+∠E1E2C+∠E2CD=540°.
则如图③中∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD为( )

如图②,同样:∠BAE1+∠AE1E2+∠E1E2C+∠E2CD=540°.
则如图③中∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD为( )

分析:由∠BAE+∠E+∠ECD=360°=2×180°,∠BAE1+∠AE1E2+∠E1E2C+∠E2CD=540°=3×180°,即可得规律:∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD=(n+1)×180°.
解答:解:∵∠BAE+∠E+∠ECD=360°=2×180°,∠BAE1+∠AE1E2+∠E1E2C+∠E2CD=540°=3×180°,
∴∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD=(n+1)×180°.
故选C.
∴∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD=(n+1)×180°.
故选C.
点评:此题考查了平行线的性质以及三角形内角和定理.此题属于规律性题目,注意观察得到规律:∠BAE1+∠AE1E2+…+∠En-1EnC+∠EnCD=(n+1)×180°是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
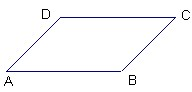 41、如图:已知;AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.
41、如图:已知;AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由. (2013•怀柔区一模)如图,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为
(2013•怀柔区一模)如图,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为 根据提示填空(或填上每步推理的理由)
根据提示填空(或填上每步推理的理由)