题目内容
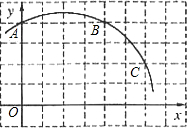 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.(1)用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
(2)若A点的坐标为(0,4),D点的坐标为(7,0),求证:直线CD是⊙M的切线.
(3)在(2)的条件下,连接MA、MC,将扇形AMC卷成一个圆锥,求此圆锥的高.
分析:(1)连接AB、BC,分别作AB、BC的垂直平分线,两条直线相交于点M;
(2)由A得到坐标是(0,4),可知B点坐标是(4,4),C点坐标是(6,2),设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD,在Rt△CME中,利用勾股定理可求CM2,同样在Rt△CED中利用勾股定理可求CD2,而根据数值可知CM2+CD2=DM2,故利用勾股定理逆定理可证△CDM是直角三角形,即∠MCD=90°,则CD是⊙M的切线;
(3)连接MA、MC,由于OA=ME=4,∠AOM=∠MEC=90°,CE=OM=2,利用SAS可证△AOM≌△MEC,再根据全等三角形的性质,易求出∠AMO+∠CME=90°,即∠AMC=90°,再利用勾股定理可求线段AM=MC=2
,从而利用弧长公式可求弧AC=
π,设扇形AMC卷成的圆锥如图3,作圆锥的高MG,连接AG,利用弧长公式可求AG=
,在Rt△AGM中,利用勾股定理可求GM.
(2)由A得到坐标是(0,4),可知B点坐标是(4,4),C点坐标是(6,2),设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD,在Rt△CME中,利用勾股定理可求CM2,同样在Rt△CED中利用勾股定理可求CD2,而根据数值可知CM2+CD2=DM2,故利用勾股定理逆定理可证△CDM是直角三角形,即∠MCD=90°,则CD是⊙M的切线;
(3)连接MA、MC,由于OA=ME=4,∠AOM=∠MEC=90°,CE=OM=2,利用SAS可证△AOM≌△MEC,再根据全等三角形的性质,易求出∠AMO+∠CME=90°,即∠AMC=90°,再利用勾股定理可求线段AM=MC=2
| 5 |
| 5 |
| ||
| 2 |
解答:(本题12分)
解:(1)如图1,点M就是要找的圆心.
正确即可(2分)
(2)证明:由A(0,4),可得小正方形的边长为1,
从而B(4,4)、C(6,2)(1分)
如图2,设过C点与x轴垂直的直线与x轴的
交点为E,连接MC,作直线CD,
∴CE=2,ME=4,ED=1,MD=5,(1分)
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,(1分)
∴∠MCD=90°,(1分)
又∵MC为半径,
∴直线CD是⊙M的切线.(1分)

(3)连接MA(图2)
∵OA=ME=4,OM=CE=2,∠AOM=∠MEC=90°,
∴△AOM≌△MEC,
∴∠AMO=∠MCE,
又∵∠CME+∠MCE=90°,∠AMO+∠CME=90°,
∴∠AMC=90°,
∴AM⊥MC,(2分)
又∵MA=MC=2
,
∴弧AC的长=
π,(1分)
设扇形AMC卷成的圆锥如图3,作圆锥的高MG,连接AG,则AG=
,(1分)
∴扇形AMC卷成的圆锥的高MG=
=
.(1分)
解:(1)如图1,点M就是要找的圆心.

正确即可(2分)
(2)证明:由A(0,4),可得小正方形的边长为1,
从而B(4,4)、C(6,2)(1分)
如图2,设过C点与x轴垂直的直线与x轴的
交点为E,连接MC,作直线CD,
∴CE=2,ME=4,ED=1,MD=5,(1分)
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,(1分)
∴∠MCD=90°,(1分)
又∵MC为半径,
∴直线CD是⊙M的切线.(1分)

(3)连接MA(图2)
∵OA=ME=4,OM=CE=2,∠AOM=∠MEC=90°,
∴△AOM≌△MEC,
∴∠AMO=∠MCE,
又∵∠CME+∠MCE=90°,∠AMO+∠CME=90°,
∴∠AMC=90°,

∴AM⊥MC,(2分)
又∵MA=MC=2
| 5 |
∴弧AC的长=
| 5 |
设扇形AMC卷成的圆锥如图3,作圆锥的高MG,连接AG,则AG=
| ||
| 2 |
∴扇形AMC卷成的圆锥的高MG=
| MA2-AG2 |
5
| ||
| 2 |
点评:本题利用了线段垂直平分线的作法、勾股定理及逆定理、切线的判定、全等三角形的判定和性质、弧长计算公式.

练习册系列答案
相关题目
 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( ) 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )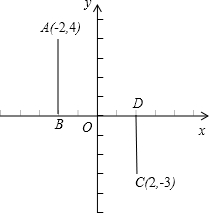 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).