题目内容
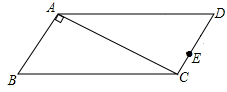
如图，∠A=∠D=90°，AC=BD，
（1）求证：AB=CD
（2）请判断△OBC的形状，并说明理由。
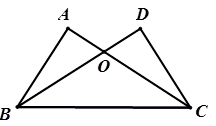
（1）求证：AB=CD
（2）请判断△OBC的形状，并说明理由。
（1）证明见解析；（2）△OBC是等腰三角形，理由见解析.
试题分析：（1）根据已知利用HL判定Rt△ABC≌Rt△DCB，证明出AB=CD；
（2）由（1）得到∠ACB=∠DBC，根据等角对等边可得到OB=OC，即△OBC是等腰三角形．
试题解析：（1）、证明： ∠A=∠D=90°（在Rt△ABC和△DCB中）
∴△ABC≌△DCB
∴AB="CD"
（2）、△OBC是等腰三角形
∵△ABC≌△DCB
∴∠OBC= ∠OCB
∴OB=OC
考点: 1.等腰三角形的判定；2.全等三角形的判定与性质.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
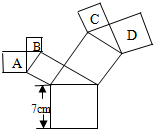
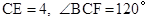，求菱形BCFE的面积．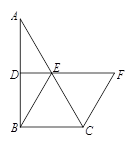
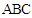中，
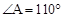，则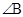
= ．
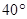，则它的底角是（ ）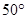
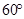
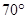
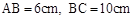，E是CD上的点，
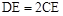．点P从D点出发，以1cm/s的速度沿DA运动至A点停止．则当△EDP为等腰三角形时，点P的运动时间为 ．
