题目内容
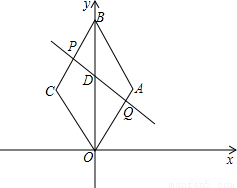
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8 ),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时,点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动设t(0<t≤8)秒后,直线PQ交OB于点D.
),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时,点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动设t(0<t≤8)秒后,直线PQ交OB于点D.(1)求∠AOB的度数及线段OA的长;
(2)求经过A,B,C三点的抛物线的解析式;
(3)当a=3,OD=
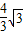 时,求t的值及此时直线PQ的解析式;
时,求t的值及此时直线PQ的解析式;(4)当a为何值时,以O,Q,D为顶点的三角形与△OAB相似?当a为何值时,以O,Q,D为顶点的三角形与△OAB不相似?请给出你的结论,并加以证明.
【答案】分析:(1)已知了∠AOC的度数,根据菱形的性质即可得出∠AOB=30°,连接AC交BO于M,在直角三角形OAM中,OM= OB,可根据OM的长和∠AOM的度数即可求出OA的长.
OB,可根据OM的长和∠AOM的度数即可求出OA的长.
(2)同(1)在直角三角形OAM中可求出AM和OM的长,即可得出A点的坐标.根据菱形的对称性,可知A、C关于y轴对称,由此可得出C点的坐标,可用待定系数法求出抛物线的解析式.
(3)当a=3时,OQ=3t,BP=t,已知了OD的长,可求出BD的长,然后根据相似三角形BPD和OQD得出的关于BM,OM,BP,OQ的比例关系式,可求出t的值.即可按(2)的方法求出Q的坐标,用待定系数法可得出直线DQ的解析式.
(4)本题要分情况讨论:
①当△ODQ∽△OBA时,PQ∥AB,四边形AQPB是平行四边形,因此BP=AQ,可据此求出a的值.
②当△ODQ∽△OAB时,∠ODQ=∠OAB.分两种情况:
一:当P、B不重合时;二:当P、B重合时.
方法一样,和(3)类似,先根据相似三角形BPD和OQD求出OD的值,然后根据相似三角形OQD和OBA求出a的值.然后进行判断即可.
解答: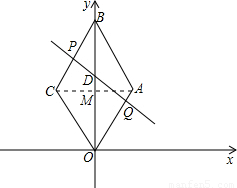 解:(1)因为四边形ABCO是菱形,∠AOC=60°,
解:(1)因为四边形ABCO是菱形,∠AOC=60°,
所以∠AOB=30°.
连接AC交OB于M,则OM= OB,AM⊥OB
OB,AM⊥OB
所以AM=tan30°×OM=4.
所以,OA=AM÷sin30°=8,
(2)由(1)可知A(4,4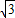 ),B(0,8
),B(0,8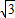 ),C(-4,4
),C(-4,4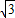 )
)
设经过A、B、C三点的抛物线为y=ax2+c
所以16a+c=4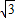 ,c=8
,c=8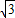 ,
,
∴a=-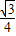
所以经过A、B、C三点的抛物线为y=- x2+8
x2+8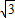
(3)当a=3时,CP=t,OQ=3t,OD=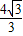 .
.
所以PB=8-t,BD=8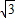 -
-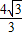 =
=
由△OQD∽△BPD得
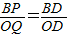
即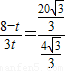 ,
,
所以t=
当t= 时,OQ=
时,OQ= .
.
同理可求Q( ,
,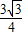 )
)
设直线PQ的解析式为y=kx+b,则
 k+b=
k+b=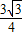 ,b=
,b=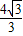 ;
;
所以k=-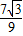
所以直线PQ的解析式为y=-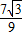 x+
x+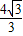 .
.
(4)当a=1时,△ODQ∽△OBA;
当1<a<3时,以O、Q、D为顶点的三角形与△OAB不能相似;
当a=1时,△ODQ∽△OBA.
理由如下:
①若△ODQ∽△OBA,可得∠ODQ=∠OBA,此时PQ∥AB.
故四边形PCOQ为平行四边形,
所以CP=OQ
即at=t(0<t≤8).
所以a=1时,△ODQ∽△OBA
②若△ODQ∽△OAB
(I)如果P点不与B点重合,此时必有△PBD∽△QOD
所以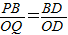
所以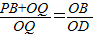 ,即
,即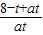 =
=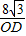 ;
;
所以OD=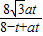 .
.
因为△ODQ∽△OAB,
所以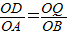 即
即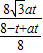 =
=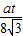
∴a=1+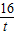 .
.
∵0<t≤8,
∴a>3,不符合题意.即a>3时,以O、Q、D为顶点的三角形与△ABO不能相似;
(II)当P与B重合时,此时D点也与B点重合.
可知此时t=8.
由△ODQ∽△OAB得 .
.
所以OB2=OA×OQ.
即(8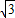 )2=8×8a
)2=8×8a
所以a=3符合题意.
故当a=1时△ODQ∽△OAB.
点评:本题是点的运动性问题,考查了菱形的性质、相似三角形的判定和性质等知识点,综合性强,难度较高.
 OB,可根据OM的长和∠AOM的度数即可求出OA的长.
OB,可根据OM的长和∠AOM的度数即可求出OA的长.(2)同(1)在直角三角形OAM中可求出AM和OM的长,即可得出A点的坐标.根据菱形的对称性,可知A、C关于y轴对称,由此可得出C点的坐标,可用待定系数法求出抛物线的解析式.
(3)当a=3时,OQ=3t,BP=t,已知了OD的长,可求出BD的长,然后根据相似三角形BPD和OQD得出的关于BM,OM,BP,OQ的比例关系式,可求出t的值.即可按(2)的方法求出Q的坐标,用待定系数法可得出直线DQ的解析式.
(4)本题要分情况讨论:
①当△ODQ∽△OBA时,PQ∥AB,四边形AQPB是平行四边形,因此BP=AQ,可据此求出a的值.
②当△ODQ∽△OAB时,∠ODQ=∠OAB.分两种情况:
一:当P、B不重合时;二:当P、B重合时.
方法一样,和(3)类似,先根据相似三角形BPD和OQD求出OD的值,然后根据相似三角形OQD和OBA求出a的值.然后进行判断即可.
解答:
 解:(1)因为四边形ABCO是菱形,∠AOC=60°,
解:(1)因为四边形ABCO是菱形,∠AOC=60°,所以∠AOB=30°.
连接AC交OB于M,则OM=
 OB,AM⊥OB
OB,AM⊥OB所以AM=tan30°×OM=4.
所以,OA=AM÷sin30°=8,
(2)由(1)可知A(4,4
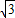 ),B(0,8
),B(0,8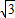 ),C(-4,4
),C(-4,4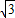 )
)设经过A、B、C三点的抛物线为y=ax2+c
所以16a+c=4
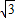 ,c=8
,c=8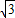 ,
,∴a=-
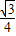
所以经过A、B、C三点的抛物线为y=-
 x2+8
x2+8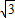
(3)当a=3时,CP=t,OQ=3t,OD=
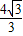 .
.所以PB=8-t,BD=8
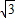 -
-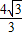 =
=
由△OQD∽△BPD得
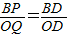
即
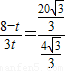 ,
,所以t=

当t=
 时,OQ=
时,OQ= .
.同理可求Q(
 ,
,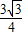 )
)设直线PQ的解析式为y=kx+b,则
 k+b=
k+b=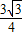 ,b=
,b=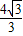 ;
;所以k=-
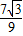
所以直线PQ的解析式为y=-
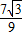 x+
x+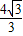 .
.(4)当a=1时,△ODQ∽△OBA;
当1<a<3时,以O、Q、D为顶点的三角形与△OAB不能相似;
当a=1时,△ODQ∽△OBA.
理由如下:
①若△ODQ∽△OBA,可得∠ODQ=∠OBA,此时PQ∥AB.
故四边形PCOQ为平行四边形,
所以CP=OQ
即at=t(0<t≤8).
所以a=1时,△ODQ∽△OBA
②若△ODQ∽△OAB
(I)如果P点不与B点重合,此时必有△PBD∽△QOD
所以
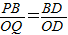
所以
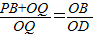 ,即
,即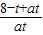 =
=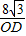 ;
;所以OD=
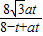 .
.因为△ODQ∽△OAB,
所以
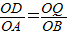 即
即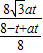 =
=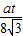
∴a=1+
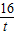 .
.∵0<t≤8,
∴a>3,不符合题意.即a>3时,以O、Q、D为顶点的三角形与△ABO不能相似;
(II)当P与B重合时,此时D点也与B点重合.
可知此时t=8.
由△ODQ∽△OAB得
 .
.所以OB2=OA×OQ.
即(8
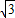 )2=8×8a
)2=8×8a所以a=3符合题意.
故当a=1时△ODQ∽△OAB.
点评:本题是点的运动性问题,考查了菱形的性质、相似三角形的判定和性质等知识点,综合性强,难度较高.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

