��Ŀ����
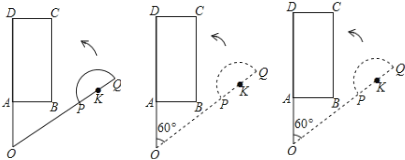
����Ŀ��ƽ���ϣ�����ABCD��ֱ��ΪQP�İ�ԲK��ͼ�ڷţ��ֱ��ӳ�DA��QP���ڵ�O������DOQ��60�㣬OQ��OD��3��OP��2��OA��AB��1�����߶�OD������ABCDλ�ù̶������߶�OQ�����Ű�ԲKһ�����ŵ�O����ʱ�뷽��ʼ��ת������ת��Ϊ��(0��ܦ���60��)��
���֣�
��1��������0�㣬����ʼλ��ʱ����P ֱ��AB��(ѡ��ڡ����ڡ�)��
����= ʱ��OQ������B��
��2����OQ��ת�����У���= ʱ����P��A��ľ�����С��PA��СֵΪ ��
��3��̽������ԲK�����ABCD�ı�����ʱ����sin����ֵ��
���𰸡���1���ڣ�15�㣻��2��60�㣬1����3��![]() ��
��![]() ��
��![]() ��
��
��������
�����������1����ͼ1��ʾ������P��PA���OD������ΪA�䣮�ڡ�A��OP��������������������Ǻ��������OA��=1����OA=1���Ӷ�����õ�A���A���غϣ����ݹ�һ������ֻ��һ��ֱ������ֱ֪�ߴ�ֱ��֪��P��AB�ϣ���ͼ2��ʾ���ɡ�ABOΪ����ֱ�������ο�֪��AOB=45�㣬�Ӷ�����á�QOQ��=15�㣻
��2����2����ͼ2������AP����OA+AP��OP����OP����A������=60��ʱ���Ⱥų�����������AP��OP-OA=2-1=1������=60��ʱ��P��A֮��ľ�����С��������ý����
��3����ԲK�����ABCD�ı����У������������
����ͼ5����ԲK��BC�����ڵ�T����ֱ��KT��AD��OQ�ij�ʼλ�����ڵ�ֱ�߷ֱ��ڵ�S��O�䣬���ǵõ���KSO=��KTB=90�㣬��KG��OO����G������Rt��OSK�������OS=![]() =2����Rt��OSO���У�SO��=OStan60��=2
=2����Rt��OSO����SO��=OStan60��=2![]() ��KO��=2
��KO��=2![]() -
-![]() 3 ��Rt��KGO��������O��= =30�㣬���KG=
3 ��Rt��KGO��������O��= =30�㣬���KG=![]() KO��=
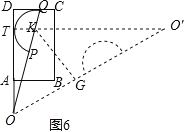
KO��=![]() ����Rt��KGO������ý�����ڵ���ԲK��AD������T����ͼ6��ͬ���ɵ�sin����ֵ�۵���ԲK��CD����ʱ����Q���D�غϣ���Ϊ�е㣬�õ���=60�����ǽ��ۿ���
����Rt��KGO������ý�����ڵ���ԲK��AD������T����ͼ6��ͬ���ɵ�sin����ֵ�۵���ԲK��CD����ʱ����Q���D�غϣ���Ϊ�е㣬�õ���=60�����ǽ��ۿ���
�����������1���ڣ�
��OQ����Bʱ����Rt��OAB�У�AO=AB��
���DOQ=��ABO=45�㣬
���=60�㩁45��=15�㣻
��2����ͼ2������AP��
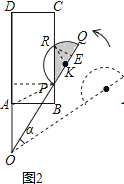
��OA+AP��OP��
��OP����A������=60��ʱ���Ⱥų�����
��AP��OP��OA=2��1=1��
�൱��=60��ʱ��P��A֮��ľ�����С��
��PA����Сֵ=1��
��3����ԲK�����ABCD�ı����У������������
����ͼ5����ԲK��BC�����ڵ�T����ֱ��KT��AD��OQ�ij�ʼλ�����ڵ�ֱ�߷ֱ��ڵ�S��O�䣬
���KSO=��KTB=90�㣬
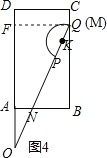
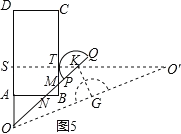
��KG��OO����G����Rt��OSK��
OS=![]() =2��
=2��
��Rt��OSO����SO��=OStan60��=2![]() ��KO��=2
��KO��=2![]() -
-![]() ��
��
��Rt��KGO���У���O��=30�㣬
��KG=![]() KO��=
KO��=![]() ��
��
����Rt��OGK��sin��=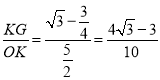 ��
��
�ڵ���ԲK��AD������T����ͼ6��ͬ���ɵ�
sin��=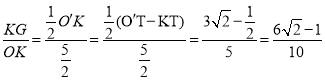 ��
��
�۵���ԲK��CD����ʱ����Q���D�غϣ���Ϊ�е㣬=60�㣬
��sin��=sin60��=![]() ��
��
��������sin����ֵΪ��![]() ��
��![]() ��
��![]() ��
��

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�