Question

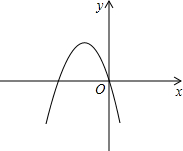（2013•安庆二模）已知二次函数y=ax²+bx+c的图象如左图所示，那么一次函数y=bx+c和反比例函数y=

a

x

在同一平面直角坐标系中的图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：根据二次函数图象开口方向与对称轴判断出a、b的正负情况，再根据二次函数图象与y轴的交点判断出c=0，然后根据一次函数图象与系数的关系，反比例函数图象与系数的关系判断出两图象的大致情况即可得解．

解答：解：∵二次函数图象开口向下，
∴a＜0，
∵对称轴x=-

b

2a

＜0，
∴b＜0，
∵二次函数图象经过坐标原点，
∴c=0，
∴一次函数y=bx+c过第二四象限且经过原点，反比例函数y=

a

x

位于第二四象限，
纵观各选项，只有C选项符合．
故选C．

点评：本题考查了二次函数图象，一次函数图象，反比例函数图象，根据二次函数图象判断出a、b、c的情况是解题的关键，也是本题的难点．