题目内容
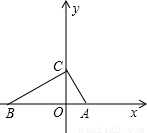
（2004•重庆）如图，在△ABC中，∠ACB=90°，AC=
，斜边AB在x轴上，点C在y轴的正半轴上，点A的坐标为（2，0）．则直角边BC所在直线的解析式为 ．
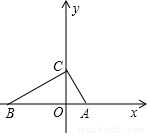
【答案】分析：根据三角形相似，对应边的比相等，可以得到B的坐标，再根据待定系数法就可以求出直线BC的解析式．
解答：解：点A的坐标为（2，0），则OA=2，
在△ABC中，∠ACB=90°，AC=
，OC⊥AB与O，
则AB=10，
则OB=8，
因而B的坐标是（-8，0），
直线BC的解析式是y=
x+4．
点评：本题主要考查了直角三角形斜边上的高线，把三角形分成的两个三角形与原三角形相似．
解答：解：点A的坐标为（2，0），则OA=2，
在△ABC中，∠ACB=90°，AC=
，OC⊥AB与O，则AB=10，
则OB=8，
因而B的坐标是（-8，0），
直线BC的解析式是y=
x+4．点评：本题主要考查了直角三角形斜边上的高线，把三角形分成的两个三角形与原三角形相似．
练习册系列答案
阅读快车系列答案
相关题目
，斜边AB在x轴上，点C在y轴的正半轴上，点A的坐标为（2，0）．则直角边BC所在直线的解析式为 ．
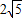，斜边AB在x轴上，点C在y轴的正半轴上，点A的坐标为（2，0）．则直角边BC所在直线的解析式为 ．