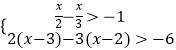题目内容
【题目】在一条直线上依次有A、B、C三个港口,A、B两港相距30千米,B、C两港相距90千米.甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.甲0.5小时到达B港,此时两船相距15千米.
求:(1)甲船何时追上乙,此时乙离C港多远?
(2)何时甲乙两船相距10千米.
【答案】(1)1小时甲追上乙,此时乙离C港60千米;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)先根据题意求得甲、乙两船的速度,然后根据甲船的路程比乙船的路程多30千米列方程求解即可;
(2)分为甲在乙的后面和甲在乙的前面两种情况列方程求解即可.
试题解析:(1)∵甲0.5小时到达B港,此时两船相距15千米, ![]() 两港相距30千米,
两港相距30千米,
∴甲船的速度为60千米/小时,乙的速度为30千米/小时.
设x小时,甲追上乙.
根据题意得:60x=30x+30,
解得:x=1.
9030×1=60千米.
答:两船出发1小时后甲船追上乙船,此时乙距离C港60千米.
(2)设x小时,甲乙两船相距10千米.
当甲在前乙在后时,60x=30+30x+10,
解得: ![]()
当甲在后乙在前时,60x=30+30x10.
解得: ![]()
答:当甲乙两船出发![]() 小时或
小时或![]() 小时后两船相距10千米.
小时后两船相距10千米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目