题目内容
如图,已知直线y=ax+b经过点A(0,-3),与x轴交于点C,且与双曲线交于点B(-4,-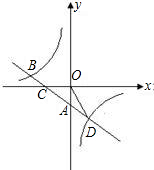 a),D.
a),D.(1)求直线和双曲线的函数关系式.
(2)求△CDO(其中O为原点)的面积.
(3)根据图象回答:当x为何值时,一次函数的函数值小于反比例函数的函数值?
分析:(1)将A(0,-3),B(-4,-a)代入直线y=ax+b,即可得出a,b的值,从而求得直线和双曲线的函数关系式.
(2)可以求得点C,D的坐标,则S△CDO=
|OC||点D纵坐标|.
(3)一次函数的函数值小于反比例函数的函数值时,即一次函数的图象在反比例函数的图象的下方时,x的取值范围即可.
(2)可以求得点C,D的坐标,则S△CDO=
| 1 |
| 2 |
(3)一次函数的函数值小于反比例函数的函数值时,即一次函数的图象在反比例函数的图象的下方时,x的取值范围即可.
解答:解:(1)由已知得
,
解为
,
∴直线解析式为y=-x-3,
设双曲线为y=
,
∵双曲线过B(-4,1),
∴1=
,
∴双曲线解析式为y=-
;
(2)由题意可知:D点为直线y=-x-3与双曲线y=-
的交点,
联立方程组
,
解得
,
因为B点坐标为(-4,1)所以D点坐标为(1,-4).
C点坐标是直线y=-x-3与x轴的交点,
令y=0,解得x=-3,故C(-3,0)
∴OC=3,
S△OCD=
×OC×yD=
×3×4=6.
(3)由图象可知,当-4<x<0或x>1时,一次函数的函数值小于反比例函数的函数值.
|
解为
|
∴直线解析式为y=-x-3,
设双曲线为y=
| k |
| x |
∵双曲线过B(-4,1),
∴1=
| k |
| -4 |
∴双曲线解析式为y=-
| 4 |
| x |
(2)由题意可知:D点为直线y=-x-3与双曲线y=-
| 4 |
| x |
联立方程组
|
解得
|
|
因为B点坐标为(-4,1)所以D点坐标为(1,-4).
C点坐标是直线y=-x-3与x轴的交点,
令y=0,解得x=-3,故C(-3,0)
∴OC=3,
S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图象可知,当-4<x<0或x>1时,一次函数的函数值小于反比例函数的函数值.
点评:本题是一道中考压轴题,考查了一次函数与反比例函数的交点问题、三角形面积的求法,以及用待定系数法求一次函数和反比例函数的解析式,是中档题,难度适中.

练习册系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )