题目内容
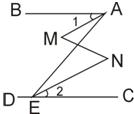 20、如图已知,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空.)
20、如图已知,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空.)解∵∠BAE+∠AED=180°(已知)
∴
AB
∥CD
( )∴∠BAE=
∠AEC
( )又∵∠1=∠2
∴∠BAE-∠1=
∠AEC
-∠2
即∠MAE=
∠AEN
∴
AM
∥EN
( )∴∠M=∠N ( )
分析:由已知易得AB∥CD,则∠BAE=∠AEC,又∠1=∠2,所以∠MAE=∠AEN,则AM∥EN,故∠M=∠N.
解答:解∵∠BAE+∠AED=180°(已知)(2空一分)
∴AB∥CD(同旁内角互补,两直线平行)
(两直线平行,内错角相等)
又∵∠1=∠2,
∴∠BAE-∠1=∠AEC-∠2,
即∠MAE=∠AEN,
∴AM∥EN,(内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
∴AB∥CD(同旁内角互补,两直线平行)
(两直线平行,内错角相等)
又∵∠1=∠2,
∴∠BAE-∠1=∠AEC-∠2,
即∠MAE=∠AEN,
∴AM∥EN,(内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
点评:此题考查平行线的判定和性质:两直线平行,内错角相等;内错角相等,两直线平行;同旁内角互补,两直线平行.要灵活应用.

练习册系列答案
相关题目
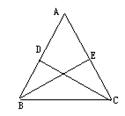
 如图已知在Rt△ABC中,∠BAC=90°,E在斜边BC上,CE=CA,求证:∠BAE=
如图已知在Rt△ABC中,∠BAC=90°,E在斜边BC上,CE=CA,求证:∠BAE=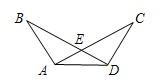 15、如图已知∠B=∠C,请同学从这①BE=CE,②AB=DC,③∠BAE=∠CDE三个等式中再选出一个作为条件,可以推出△AED是等腰三角形的有
15、如图已知∠B=∠C,请同学从这①BE=CE,②AB=DC,③∠BAE=∠CDE三个等式中再选出一个作为条件,可以推出△AED是等腰三角形的有 如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.
如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.