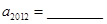题目内容
探究与思考:
①现定义某种运算“*”,对任意两个有理数a、b,有a*b=ab,如(-3)*2=(-3)2=9.
试计算: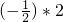 =______,(-1)*(2*3)=______.
=______,(-1)*(2*3)=______.
②现有若干个数,第1个数记为a1,第二个数记为a2,第三个数记为a3…,第n个数记为an,若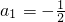 ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数.”
,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数.”
(1)试计算a2=______,a3=______,a4=______.
(2)根据以上结果,请你写出a2011=______,a2012=______.
解:①(- )*2=(-
)*2=(- )2=
)2= ,
,
(-1)*(2*3)=(-1)*(23)=(-1)*8=(-1)8=1;
②(1)a2= =
= ,a3=
,a3=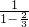 =3,a4=
=3,a4=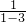 =-
=- ,则a5=
,则a5= ;
;
(2)根据循环的规律可以得到:a2011=- ,a2012=
,a2012= .
.
故答案是:① 、1;②(1)
、1;②(1) 、3.-
、3.- ;(2)-
;(2)- 、
、 .
.
分析:①根据运算的定义首先转化成一般的运算,然后计算即可求解;
②根据每个数都等于“1与它前面的那个数的差的倒数,列出式子即可求解,根据解得的结果的规律即可解决(2).
点评:本题考查了有理数的运算,是定义新运算题型.直接把对应的数字代入所给的式子可求出所要的结果.解题关键是对号入座不要找错对应关系.
 )*2=(-
)*2=(- )2=
)2= ,
,(-1)*(2*3)=(-1)*(23)=(-1)*8=(-1)8=1;
②(1)a2=
 =
= ,a3=
,a3=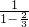 =3,a4=
=3,a4=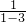 =-
=- ,则a5=
,则a5= ;
;(2)根据循环的规律可以得到:a2011=-
 ,a2012=
,a2012= .
.故答案是:①
 、1;②(1)
、1;②(1) 、3.-
、3.- ;(2)-
;(2)- 、
、 .
.分析:①根据运算的定义首先转化成一般的运算,然后计算即可求解;
②根据每个数都等于“1与它前面的那个数的差的倒数,列出式子即可求解,根据解得的结果的规律即可解决(2).
点评:本题考查了有理数的运算,是定义新运算题型.直接把对应的数字代入所给的式子可求出所要的结果.解题关键是对号入座不要找错对应关系.

练习册系列答案
相关题目
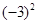 =9.
=9.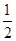 )*2 = , (-1)*(2*3)= .
)*2 = , (-1)*(2*3)= .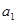 ,第二个数记为
,第二个数记为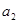 ,第三个数记为
,第三个数记为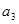 ……,第n个数记为
……,第n个数记为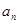 ,若
,若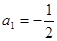 ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
 ,
,
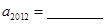
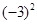 =9.
=9. )*2
= , (-1)*(2*3)= .
)*2
= , (-1)*(2*3)= .  ,第二个数记为
,第二个数记为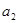 ,第三个数记为
,第三个数记为 ……,第n个数记为
……,第n个数记为 ,若
,若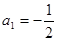 ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
 ,
,