题目内容
（2013•襄阳）如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）分析：由平行四边形的性质和已知条件计算即可，解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体．
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD=5，
∵△OCD的周长为23，
∴OD+OC=23-5=18，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=36，
故选C．
∴AB=CD=5，
∵△OCD的周长为23，
∴OD+OC=23-5=18，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=36，
故选C．
点评：本题主要考查了平行四边形的基本性质，并利用性质解题．平行四边形的基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．
练习册系列答案
巧学巧练系列答案
相关题目
（2013•襄阳）如图，BD平分∠ABC，CD∥AB，若∠BCD=70°，则∠ABD的度数为（ ）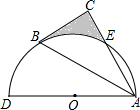
（2013•襄阳）如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为
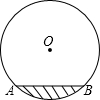（2013•襄阳）如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB为0.8m，则排水管内水的深度为
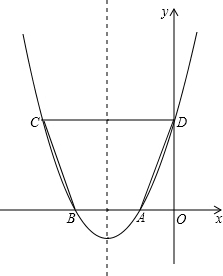（2013•襄阳）如图，已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（-1，0），对称轴为直线x=-2．