Question

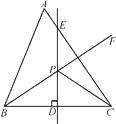
【题目】(12分)如图，在△ABC中，∠A＝60°，点D是BC边的中点，DE⊥BC，∠ABC的平分线BF交DE于△ABC内一点P，连接PC.

(1)若∠ACP＝24°，求∠ABP的度数；

(2)若∠ACP＝m°，∠ABP＝n°，请直接写出m，n满足的关系式：_________________．

Answer 1

【答案】(1)∠ABP＝32° (2) m＋3n＝120

【解析】试题分析：（1）根据线段垂直平分线的性质，可得∠PBC=∠PCB，根据角平分线的定义，可得∠PBC=∠PCB=∠ABP，最后根据三角形内角和定理，即可得到∠ABP的度数；

（2）运用（1）中的方法，即可得出m，n满足的关系式．

试题解析：(1)∵点D是BC边的中点，DE⊥BC，

∴PB=PC，

∴∠PBC=∠PCB，

∵BP平分∠ABC，

∴∠PBC=∠ABP，

∴∠PBC=∠PCB=∠ABP，

∵∠A=60°，∠ACP=24°，

∴∠PBC+∠PCB+∠ABP=120°24°，

∴3∠ABP=120°24°，

∴∠ABP=32°；

（2）∵点D是BC边的中点，DE⊥BC，

∴PB=PC，

∴∠PBC=∠PCB，

∵BP平分∠ABC，

∴∠PBC=∠ABP，

∴∠PBC=∠PCB=∠ABP=n°，

∵∠A=60°,∠ACP=m°，

∴∠PBC+∠PCB+∠ABP=120°m°，

∴3∠ABP=120°m°，

∴3n°+m°=120°，

故答案为：m+3n=120.