��Ŀ����
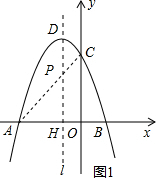
��2013•�Ű�����ͼ����֪������y=ax2+bx+c����A��-3��0����B��1��0����C��0��3�����㣬�䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P�Ǹ������߶Գ���l�ϵ�һ�����㣬���PBC�ܳ�����Сֵ��
��3����ͼ��2������E���߶�AD�ϵ�һ�����㣨 E��A��D���غϣ�����E����ƽ����y���ֱ�߽��������ڵ�F����x���ڵ�G�����E�ĺ�����Ϊm����ADF�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ�������ֵ�������ڣ�������ֵ����ʱ��E�����ꣻ �������ڣ���˵�����ɣ�

��1����������ߵĽ���ʽ��
��2������P�Ǹ������߶Գ���l�ϵ�һ�����㣬���PBC�ܳ�����Сֵ��
��3����ͼ��2������E���߶�AD�ϵ�һ�����㣨 E��A��D���غϣ�����E����ƽ����y���ֱ�߽��������ڵ�F����x���ڵ�G�����E�ĺ�����Ϊm����ADF�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ�������ֵ�������ڣ�������ֵ����ʱ��E�����ꣻ �������ڣ���˵�����ɣ�

��������1�����ݺ���ͼ�������㣬�ô���ϵ����ȷ�����κ����Ľ���ʽ���ɣ�
��2������BC�Ƕ�ֵ���õ���PB+PC��Сʱ����PBC���ܳ���С�����ݵ�����������Ӧ�߶εij����ɣ�
��3�����E�ĺ�����Ϊm����ʾ��E��m��2m+6����F��m��-m2-2m+3��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɣ�
��2������BC�Ƕ�ֵ���õ���PB+PC��Сʱ����PBC���ܳ���С�����ݵ�����������Ӧ�߶εij����ɣ�
��3�����E�ĺ�����Ϊm����ʾ��E��m��2m+6����F��m��-m2-2m+3��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɣ�
��� �⣺��1���������֪��
�⣺��1���������֪��
��ã�
�������ߵĽ���ʽΪ��y=-x2-2x+3��
��2���ߡ�PBC���ܳ�Ϊ��PB+PC+BC
��BC�Ƕ�ֵ��
�൱PB+PC��Сʱ����PBC���ܳ���С��
�ߵ�A����B���ڶԳ���l�Գƣ�
������AC��l�ڵ�P������PΪ����ĵ�
��AP=BP
���PBC���ܳ���С�ǣ�PB+PC+BC=AC+BC
��A��-3��0����B��1��0����C��0��3����
��AC=3
��BC=
��
�ʡ�PBC�ܳ�����СֵΪ3
+
��
��3���١�������y=-x2-2x+3����D������Ϊ��-1��4��
��A��-3��0��
��ֱ��AD�Ľ���ʽΪy=2x+6
�ߵ�E�ĺ�����Ϊm��
��E��m��2m+6����F��m��-m2-2m+3��
��EF=-m2-2m+3-��2m+6��
=-m2-4m-3
��S=S��DEF+S��AEF
=
EF•GH+
EF•AG
=
EF•AH
=
��-m2-4m-3����2
=-m2-4m-3��
��S=-m2-4m-3
=-��m+2��2+1��
�൱m=-2ʱ��S������ֵΪ1
��ʱ��E������Ϊ��-2��2����
 �⣺��1���������֪��
�⣺��1���������֪��
|
��ã�
|
�������ߵĽ���ʽΪ��y=-x2-2x+3��
��2���ߡ�PBC���ܳ�Ϊ��PB+PC+BC
��BC�Ƕ�ֵ��
�൱PB+PC��Сʱ����PBC���ܳ���С��
�ߵ�A����B���ڶԳ���l�Գƣ�
������AC��l�ڵ�P������PΪ����ĵ�
��AP=BP
���PBC���ܳ���С�ǣ�PB+PC+BC=AC+BC
��A��-3��0����B��1��0����C��0��3����
��AC=3
| 2 |
| 10 |
�ʡ�PBC�ܳ�����СֵΪ3
| 2 |
| 10 |
��3���١�������y=-x2-2x+3����D������Ϊ��-1��4��
��A��-3��0��
��ֱ��AD�Ľ���ʽΪy=2x+6
�ߵ�E�ĺ�����Ϊm��
��E��m��2m+6����F��m��-m2-2m+3��
��EF=-m2-2m+3-��2m+6��
=-m2-4m-3
��S=S��DEF+S��AEF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-m2-4m-3��
��S=-m2-4m-3
=-��m+2��2+1��
�൱m=-2ʱ��S������ֵΪ1
��ʱ��E������Ϊ��-2��2����
������������Ҫ�����˴���ϵ��������κ�������ʽ�Լ����κ�������ֵ�����ݵ�������ʾ���߶εij��DZ�ʾ�������ε�����Ļ�����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2013•�Ű�����ͼ��DE�ǡ�ABC����λ�ߣ��ӳ�DE��FʹEF=DE������CF����S��CEF��S�ı���BCED��ֵΪ��������
��2013•�Ű�����ͼ��DE�ǡ�ABC����λ�ߣ��ӳ�DE��FʹEF=DE������CF����S��CEF��S�ı���BCED��ֵΪ��������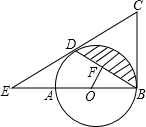 ��2013•�Ű�����ͼ��AB�ǡ�O��ֱ����BCΪ��O�����ߣ�DΪ��O�ϵ�һ�㣬CD=CB���ӳ�CD��BA���ӳ����ڵ�E��
��2013•�Ű�����ͼ��AB�ǡ�O��ֱ����BCΪ��O�����ߣ�DΪ��O�ϵ�һ�㣬CD=CB���ӳ�CD��BA���ӳ����ڵ�E��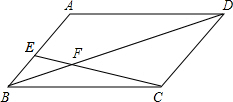 ��2013•�Ű�����ͼ����?ABCD�У�E��AB�ϣ�CE��BD����F����AE��BE=4��3����BF=2����DF=
��2013•�Ű�����ͼ����?ABCD�У�E��AB�ϣ�CE��BD����F����AE��BE=4��3����BF=2����DF=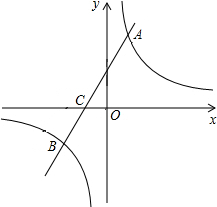 ��2013•�Ű�����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������y=
��2013•�Ű�����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������y=