题目内容
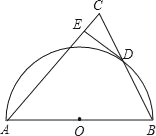
【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
【答案】(1)![]() 与
与![]() 相切;(2)
相切;(2)![]()
【解析】
(1)先证明OD为△ABC的中位线得到OD∥AC,再利用DE⊥AC得到OD⊥DE,然后根据切线的判定方法可确定DE为⊙O的切线;
(2)作OF⊥AC于F,如图,证明四边形ODEF为矩形得到OF=DE,再证明△OAF为等腰直角三角形得到OF=![]() ,从而得到DE的长.
,从而得到DE的长.
(1)DE与⊙O相切.理由如下:
连接OD.
∵CD=BD,OA=OB,∴OD为△ABC的中位线,∴OD∥AC.
∵DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线;
(2)作OF⊥AC于F,如图,易得四边形ODEF为矩形,∴OF=DE.
∵∠BAC=45°,∴△OAF为等腰直角三角形,∴OF=![]() OA=
OA=![]() ,∴DE=
,∴DE=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目