题目内容
【题目】【结论再现】
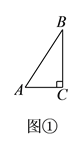
(![]() )如图①,在
)如图①,在![]() 中,
中, ![]() ,
, ![]() ,则
,则![]() __________
__________![]() ,
, ![]() __________.
__________.
【问题解决】
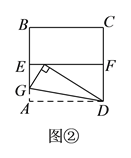
(![]() )如图②,四边形
)如图②,四边形![]() 是一张边长为
是一张边长为![]() 的正方形纸片,
的正方形纸片, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,沿过点
的中点,沿过点![]() 的折痕将纸片翻折,使点
的折痕将纸片翻折,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕交
处,折痕交![]() 于点
于点![]() ,求
,求![]() 的度数和
的度数和![]() 的长.
的长.
【问题探究】
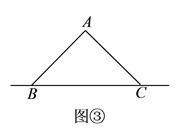
(![]() )如图③,点
)如图③,点![]() 是等腰
是等腰![]() 斜边
斜边![]() 所在直线上一点,且满足
所在直线上一点,且满足![]() ,求
,求![]() 的大小和此时
的大小和此时![]() 的值.
的值.
【答案】(![]() )30,
)30, ![]() ;(
;(![]() )
)![]() ,
, ![]()
![]() ;(
;(![]() )
)![]() 的度数为
的度数为![]() 或
或![]() ,
, ![]() .
.
【解析】试题分析:(1)通过求∠B 的正弦和正切即可得;
(2)根据正方形的性质,即可得∠C=∠A=90°,AD=BC=CD=AB,又由E、F分别为AB、CD的中点,即可得在Rt△A′DF中,由sin∠FA′D=![]() =
=![]() ,即可求得∠DA′F的度数,再由平角即可得
,即可求得∠DA′F的度数,再由平角即可得![]() 的度数,再利用勾股定理通过计算即可得BG的长;
的度数,再利用勾股定理通过计算即可得BG的长;
(3)分①点D 在BC边上,②点D 在BC延长线上,两种情况通过讨论即可得.
试题解析:(![]() )
)![]() ;
; ![]() .
.
(![]() )∵
)∵![]() 折叠后得到
折叠后得到![]() ,∴
,∴![]() ,且
,且![]() ,
,
∴在![]() 中,
中, ![]() ,sin∠FA′D=
,sin∠FA′D=![]() =
=![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,∴
,∴![]() ,
,
又∵在![]() 中,
中, ![]() ,那么
,那么![]() ,
,
∴![]() ,∴
,∴![]() ,
,
则![]() ,那么
,那么![]()
![]()
![]() .
.
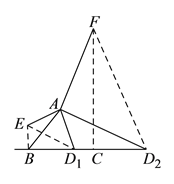
(![]() )如图,①当
)如图,①当![]() 在
在![]() 边上时,将线段
边上时,将线段![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,
与(![]() )同理可证
)同理可证![]() ≌
≌![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴四边形
,∴四边形![]() .
. ![]() 、
、![]() .
. ![]() 四点共圆,∴
四点共圆,∴![]() ,
,
∴![]() .
.
②当![]() 在
在![]() 延长线上时,将线段
延长线上时,将线段![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
同理可证: ![]() ,
,
∵![]() ,∴四边形
,∴四边形![]() .
. ![]() .
. ![]() 、
、![]() 四点共圆,∴
四点共圆,∴![]() ,
,
∴![]() ,
,
综上, ![]() 的度数为
的度数为![]() 或
或![]() .
.
比值计算如下:
过点![]() 作
作![]() ,如图,
,如图,
则在![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
设![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
