题目内容
等边三角形的外接圆面积是内切圆面积的（ ）A．2倍
B．3倍
C．4倍
D．5倍
【答案】分析：根据等边三角形的三线合一，可以发现并证明等边三角形的外接圆半径是内切圆半径的2倍．再根据圆的面积公式，得出其外接圆的面积是内切圆面积的4倍．
解答：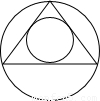
解：因为等边三角形的三线合一，所以圆心为其重心，即外接圆的半径是内接圆半径的2倍，所以外接圆面积是内切圆面积的4倍．
故选C．
点评：本题需要注意：等边三角形的外接圆的半径是内切圆的半径的2倍．
解答：
解：因为等边三角形的三线合一，所以圆心为其重心，即外接圆的半径是内接圆半径的2倍，所以外接圆面积是内切圆面积的4倍．故选C．
点评：本题需要注意：等边三角形的外接圆的半径是内切圆的半径的2倍．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC是边长为a的等边三角形，O为△ABC的中心．将△ABC绕着中心O旋转120°．
如图，△ABC是边长为a的等边三角形，O为△ABC的中心．将△ABC绕着中心O旋转120°．