题目内容
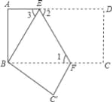
【题目】如图,已知把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
(1)求∠2,∠3的度数.
(2)求长方形ABCD的纸片的面积S.
【答案】(1)60°(2)![]()
【解析】
(1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=2,在Rt△ABE中,根据直角三角形的性质就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.
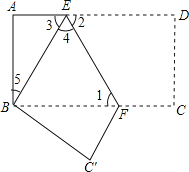
解:(1)∵AD∥BC,
∴∠2=∠1=60°,
又∵∠4=∠2=60°,
∴∠3=180°-60°-60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°-60°=30°;
∴BE=2AE=4,
∴AB=2![]()
∴AD=AE+DE=AE+BE=2+4=6,
∴长方形纸片ABCD的面积S为:ABAD=2![]() ×6=12
×6=12![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目





