Question

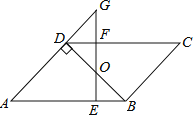
【题目】如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．

（1）求证：AE=EF．

（2）如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点 ”其余条件不变，那么结论AE=EF是否成立呢？若成立，请你证明这一结论，若不成立，请你说明理由．

Answer 1

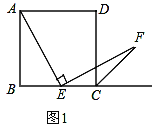
【答案】（1）证明见解析；（2）成立，证明见解析

【解析】试题分析：（1）取AB的中点G，连接EG，根据已知条件利用ASA判定△AME≌△ECF，因为全等三角形的对应边相等，所以AE=EF．
（2）在AB上取一点M，使AM=EC，连接ME，根据已知条件利用ASA判定△AME≌△ECF，因为全等三角形的对应边相等，所以AE=EF．

试题解析：

（1）证明：取AB的中点G，连接EG

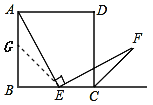
∵四边形ABCD是正方形∴AB=BC，∠B=∠BCD=∠DCG=90°

∵点E是边BC的中点

∴AM=EC=BE

∴∠BGE=∠BEG=45°

∴∠AGE=135°，

∵CF平分∠DCG，

∴∠DCF=∠FCG=45°，

∴∠ECF=180°－∠FCG=135°，

∴∠AGE=∠ECF

∵∠AEF=90°

∴∠AEB+∠CEF=90°，

又∵∠AEB+∠GAE=90°，

∴∠GAE=∠CEF，

在△AGE和△ECF中，∠GAE=∠CEF，AG=CE，∠AGE=∠ECF∴△AGE≌△ECF（ASA），∴AE=EF

（2）证明：在AB上取一点M，使AM=EC，连结ME，

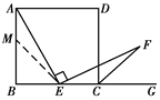
∴BM=BE∴∠BME=45°∴∠AME=135°.

∵CF是外角平分线，

∴∠DCF = 45°.

∴∠ECF = 135°.

∴∠AME = ∠ECF .

∵∠AEB +∠BAE=90°，∠AEB + ∠CEF = 90°,

∴∠BAE = ∠CEF.

∴△AME ≌ △ECF（ASA).

∴AE=EF.