题目内容
6、如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（ ）分析：根据正方形的面积公式，结合勾股定理，能够导出正方形A，B，C，D的面积和即为最大正方形的面积．
解答：
解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2=S3，于是S3=S1+S2，
即S3=9+25+4+9=47．
故选C．
解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2=S3，于是S3=S1+S2，即S3=9+25+4+9=47．
故选C．
点评：能够发现正方形A，B，C，D的边长正好是两个直角三角形的四条直角边，根据勾股定理最终能够证明正方形A，B，C，D的面积和即是最大正方形的面积．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
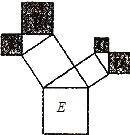如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是
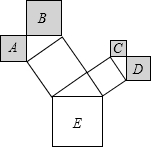（2013•莆田）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别为2，5，1，2．则最大的正方形E的面积是
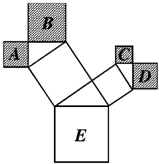如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是4、6、3、4，则最大正方形E的面积是（ ）
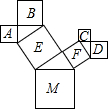如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若最大正方形M的边长是3，则正方形A、B、C、D、E、F的面积之和是