题目内容
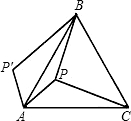 如图所示,P是正三角形ABC内一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为
如图所示,P是正三角形ABC内一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为
- A.4
- B.8
- C.10
- D.6
D
分析:连接PP′,由旋转的性质可知,P′A=PA=6,P′B=PB=8,∠P′AP=60°,可证△P′AP为等边三角形,则P′P=PA.
解答: 解:连接PP′,由旋转的性质可知,P′A=PA=6,∠BAP'=∠CAP,
解:连接PP′,由旋转的性质可知,P′A=PA=6,∠BAP'=∠CAP,
∵∠BAP=∠BAP,
故可得:∠P′AP=∠BAC=60°,
∴△P′AP为等边三角形,
∴P′P=PA=6.
故选D.
点评:本题考查了旋转的性质,等边三角形的判定与性质.关键是通过旋转,得出旋转角及对应边的关系,判断特殊三角形.
分析:连接PP′,由旋转的性质可知,P′A=PA=6,P′B=PB=8,∠P′AP=60°,可证△P′AP为等边三角形,则P′P=PA.
解答:
 解:连接PP′,由旋转的性质可知,P′A=PA=6,∠BAP'=∠CAP,
解:连接PP′,由旋转的性质可知,P′A=PA=6,∠BAP'=∠CAP,∵∠BAP=∠BAP,
故可得:∠P′AP=∠BAC=60°,
∴△P′AP为等边三角形,
∴P′P=PA=6.
故选D.
点评:本题考查了旋转的性质,等边三角形的判定与性质.关键是通过旋转,得出旋转角及对应边的关系,判断特殊三角形.

练习册系列答案
相关题目