题目内容
(2013•竹溪县模拟)如图1,已知双曲线y=
与直线y=
x交于A,B两点,点A在第一象限,点A的横坐标为4.
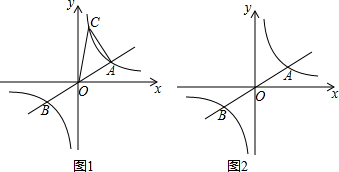
(1)求k的值;
(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;
(3)如图2,过原点的另一条直线交双曲线于P、Q两点,若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
| k |
| x |
| 1 |
| 2 |

(1)求k的值;
(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;
(3)如图2,过原点的另一条直线交双曲线于P、Q两点,若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
分析:(1)将x=4代入一次函数解析式求出y的值,确定出A的坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)将C纵坐标代入反比例解析式求出横坐标,确定出C坐标,即CD与OD的长,三角形AAOC面积=三角形COD面积+梯形AEDC面积-三角形AOE面积,求出即可;
(3)设P(x,
),即OM=x,PM=
,分四种情况考虑:若P在A的左侧,如图所示,作PM⊥x轴,AN⊥x轴,由四边形APBQ面积为24,且为平行四边形,得到三角形AOP面积为6,根据三角形POM面积+梯形ANMP面积-三角形AON面积,列出关于x的方程,求出方程的解得到x的值,确定出此时P的坐标;若交点P在第三象限,Q在第一象限,利用对称性求出P坐标即可;若P在A的右侧,同理可得P的坐标;若交点P在第三象限,Q在第一象限,利用对称性求出P的坐标.
(2)将C纵坐标代入反比例解析式求出横坐标,确定出C坐标,即CD与OD的长,三角形AAOC面积=三角形COD面积+梯形AEDC面积-三角形AOE面积,求出即可;
(3)设P(x,
| 8 |
| x |
| 8 |
| x |
解答: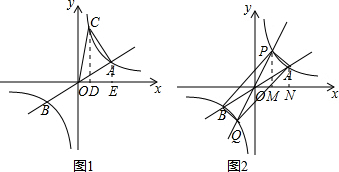
解:(1)将x=4代入y=
x=2,即A(4,2),
将A(4,2)代入反比例解析式得:k=8;
(2)过C作CD⊥x轴,作AE⊥x轴,
将y=8代入反比例解析式得:x=1,即C(1,8),
∴OD=1,CD=8,
∵A(4,2),∴OE=4,AE=2,
∵S△AOC=S△COD+S梯形AEDC-S△AOE=
×1×8+
×(2+8)×3-
×4×2=15;
(3)设P(x,
),即OM=x,PM=
,
若P在A的左侧,如图所示,作PM⊥x轴,AN⊥x轴,
∵由点A、B、P、Q为顶点的四边形面积为24,OP=OQ,OA=OB,即四边形APBQ为平行四边形,
∴S△AOP=S△POM+S梯形ANMP-S△AON=
×24=6,即
x•
+
×(4-x)×(2+
)-4=6,
解得:x=2,即P(2,4);
若交点P在第三象限,Q在第一象限,此时P(-2,-4);
若P在A的右侧,同理可得4+
×(x-4)×(2+
)-4=6,
解得:x=8,此时P坐标为(8,1);
若交点P在第三象限,Q在第一象限,此时P坐标为(-8,-1),
综上,P坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).

解:(1)将x=4代入y=
| 1 |
| 2 |
将A(4,2)代入反比例解析式得:k=8;
(2)过C作CD⊥x轴,作AE⊥x轴,
将y=8代入反比例解析式得:x=1,即C(1,8),
∴OD=1,CD=8,
∵A(4,2),∴OE=4,AE=2,
∵S△AOC=S△COD+S梯形AEDC-S△AOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)设P(x,
| 8 |
| x |
| 8 |
| x |
若P在A的左侧,如图所示,作PM⊥x轴,AN⊥x轴,
∵由点A、B、P、Q为顶点的四边形面积为24,OP=OQ,OA=OB,即四边形APBQ为平行四边形,
∴S△AOP=S△POM+S梯形ANMP-S△AON=
| 1 |
| 4 |
| 1 |
| 2 |
| 8 |
| x |
| 1 |
| 2 |
| 8 |
| x |
解得:x=2,即P(2,4);
若交点P在第三象限,Q在第一象限,此时P(-2,-4);
若P在A的右侧,同理可得4+
| 1 |
| 2 |
| 8 |
| x |
解得:x=8,此时P坐标为(8,1);
若交点P在第三象限,Q在第一象限,此时P坐标为(-8,-1),
综上,P坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
点评:此题考查了反比例综合题,涉及的知识有:坐标与图形性质,三角形、梯形的面积,以及待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
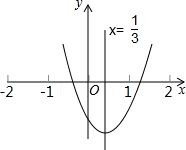 (2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断:
(2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断: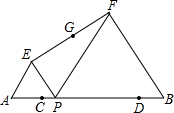 (2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是
(2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是