题目内容
(12分)用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
现配制这种饮料10千克,,要求至少含有4000单位的维生素C,并且购买甲、乙两种原料的费用不超过72元,若购买甲种原料的质量为x(整数)千克,请解答下列问题:
(1)购买甲、乙两种原料有哪几种方案?
(2)哪种购买方案的费用最低?最低费用是多少元?
| 原料 维生素及价格 | 甲种原料 | 乙种原料 |
| 维生素C/(单位/千克) | 600 | 100 |
| 原料价格/(元/千克) | 8 | 4 |
(1)购买甲、乙两种原料有哪几种方案?
(2)哪种购买方案的费用最低?最低费用是多少元?
(1)方案一:购买甲种原料6千克,乙种原料4千克;
方案二:购买甲种原料7千克,乙种原料3千克;
方案三:购买甲种原料8千克,乙种原料2千克.
(2)方案一的费用最低,最低费用为64元
方案二:购买甲种原料7千克,乙种原料3千克;
方案三:购买甲种原料8千克,乙种原料2千克.
(2)方案一的费用最低,最低费用为64元
(1)根据题意得
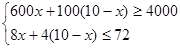
解得6≤x≤8
∵x为整数,∴购买甲、乙两种原料共有3种方案如下:
方案一:购买甲种原料6千克,乙种原料4千克;
方案二:购买甲种原料7千克,乙种原料3千克;
方案三:购买甲种原料8千克,乙种原料2千克.
(2)各种方案的费用如下:
方案一:6×8+4×4=64(元);方案二:7×8+3×4=68(元);
方案三:8×8+2×4=72(元)
∴方案一的费用最低,最低费用为64元
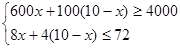
解得6≤x≤8
∵x为整数,∴购买甲、乙两种原料共有3种方案如下:
方案一:购买甲种原料6千克,乙种原料4千克;
方案二:购买甲种原料7千克,乙种原料3千克;
方案三:购买甲种原料8千克,乙种原料2千克.
(2)各种方案的费用如下:
方案一:6×8+4×4=64(元);方案二:7×8+3×4=68(元);
方案三:8×8+2×4=72(元)
∴方案一的费用最低,最低费用为64元

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
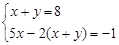
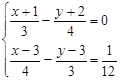
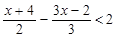
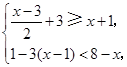 (在数轴上表示解集并写出符合的整数解)
(在数轴上表示解集并写出符合的整数解)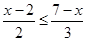 的正整数解是-----------。
的正整数解是-----------。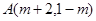 位于第二象限,那么
位于第二象限,那么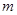 的取值为___________。
的取值为___________。 的解集为
的解集为 ,则有 ( )
,则有 ( )



 时,
时,
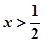 时,
时, 时,
时, 时,
时, 时,不等式
时,不等式 的解集为
的解集为

