题目内容
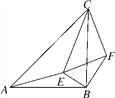
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
【答案】(1)见解析 (2)![]()
证明:∵△ABC和△CEF均为等腰直角三角形,∴![]() ,∠ACB=∠ECF=45°
,∠ACB=∠ECF=45°
∵∠ACB=∠ACE+∠BCE,∠ECF=∠BCF+∠BCE,∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)解:由(1)可知△CAE∽△CBF,∴∠CAE=∠CBF,![]() .又∵AE=2,∴
.又∵AE=2,∴![]() =
=![]() ,∴BF=
,∴BF=![]() ∵∠CAE+∠CBE=90°,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2=12+(![]() )2=3,
)2=3,
∴EF=![]() ,∴CE=
,∴CE=![]() EF=
EF=![]() .
.
【解析】试题分析:![]() 首先由△ABC和△CEF均为等腰直角三角形可得
首先由△ABC和△CEF均为等腰直角三角形可得![]() ∠ACB=∠ECF=45°.然后根据相似三角形判定的方法,推得△CAE∽△CBF即可.
∠ACB=∠ECF=45°.然后根据相似三角形判定的方法,推得△CAE∽△CBF即可.
![]() 首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据
首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据![]() 判断出
判断出![]() ,然后在
,然后在![]() 中,根据勾股定理,求出
中,根据勾股定理,求出![]() 的长度,再根据
的长度,再根据![]() 的关系,求出
的关系,求出![]() 的长即可.
的长即可.
试题解析:∵△ABC和△CEF均为等腰直角三角形,
![]() ∠ACB=∠ECF=45°.
∠ACB=∠ECF=45°.
∵∠ACB=∠ACE+∠BCE,∠ECF=∠BCF+∠BCE,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2)由(1)可知△CAE∽△CBF,
∴∠CAE=∠CBF, ![]()
又∵AE=2,![]()
![]()
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
![]()
![]()
![]()

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目