题目内容
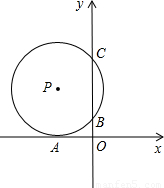
(2006•贺州)如图,⊙P与x轴相切于A,与y轴相交于B(0,2),C(0,8),求经过A,C两点的直线解析式.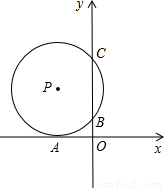
【答案】分析:先根据切割线定理求出A点坐标,再用待定系数法求出经过A,C两点的直线解析式.
解答:解:∵⊙P与x轴相切于A,
∴OA,OC分别是⊙P的切线和割线,
故OA2=OB•OC,
∵B、C两点的坐标分别为B(0,2),C(0,8),
∴OB=2、OC=8,
故OA2=2×8=16,OA=±4,
又∵A在x轴的负半轴,所以A点坐标为(-4,0);
设过A、C两点的一次函数的解析式为y=kx+b(k≠0),
把A(-4,0),C(0,8)代入得: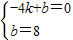 ,
,
解得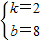 ,
,
故经过A,C两点的直线解析式为:y=2k+8.
点评:此题考查的是切割线定理及用待定系数法求一次函数的解析式,比较简单.
解答:解:∵⊙P与x轴相切于A,
∴OA,OC分别是⊙P的切线和割线,
故OA2=OB•OC,
∵B、C两点的坐标分别为B(0,2),C(0,8),
∴OB=2、OC=8,
故OA2=2×8=16,OA=±4,
又∵A在x轴的负半轴,所以A点坐标为(-4,0);
设过A、C两点的一次函数的解析式为y=kx+b(k≠0),
把A(-4,0),C(0,8)代入得:
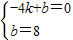 ,
,解得
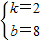 ,
,故经过A,C两点的直线解析式为:y=2k+8.
点评:此题考查的是切割线定理及用待定系数法求一次函数的解析式,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

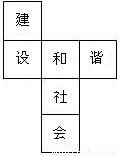 (2006•贺州)如图是一个正方体的展开图,将它折叠成正方体后,“建”字的对面是( )
(2006•贺州)如图是一个正方体的展开图,将它折叠成正方体后,“建”字的对面是( )