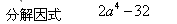题目内容
在下面三小题中任选其中两小题完成:(1)已知a+b=2,求代数式a2-b2+4b的值;
(2)分解因式2a4-32
(3)已知
| x |
| y |
| 2 |
| 3 |
| 2x-y |
| x+2y |
分析:(1)将a2-b2因式分解,把a+b=2代入计算,再求整个式子的值;
(2)提公因式2,再利用平方差公式因式分解;
(3)由已知设x=2k,y=3k,代入分式化简即可.
(2)提公因式2,再利用平方差公式因式分解;
(3)由已知设x=2k,y=3k,代入分式化简即可.
解答:解:(1)∵a+b=2
∴a2-b2+4b=(a-b)(a+b)+4b
=2(a-b)+4b=2a-2b+4b
=2a+2b=2(a+b)=2×2=4;
(2)2a4-32=2(a4-16)
=2(a2+4)(a2-4)
=2(a2+4)(a-2)(a+2);
(3)∵
=
,不妨设x=2k,y=3k,
∴
=
=
;
∴a2-b2+4b=(a-b)(a+b)+4b
=2(a-b)+4b=2a-2b+4b
=2a+2b=2(a+b)=2×2=4;
(2)2a4-32=2(a4-16)
=2(a2+4)(a2-4)
=2(a2+4)(a-2)(a+2);
(3)∵
| x |
| y |
| 2 |
| 3 |
∴
| 2x-y |
| x+2y |
| 4k-3k |
| 2k+6k |
| 1 |
| 8 |
点评:本题考查了因式分解及分式的化简.因式分解要分解到不能再分解为止,分式的化简可以考虑换元法,使运算简便.

练习册系列答案
相关题目

 ,求代数式
,求代数式 的值【小题2】(2)
的值【小题2】(2) 

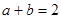 ,求代数式
,求代数式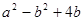 的值
的值