题目内容
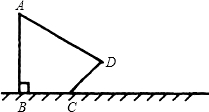 如图,电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,若CD与地面成45°,∠A=60°,CD=4m,BC=(4
如图,电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,若CD与地面成45°,∠A=60°,CD=4m,BC=(4| 6 |
| 2 |
分析:延长AD交地面于E,作DF⊥BE于F,求出BE=BC+CF+FE=6
,根据正切求出AB的值即可.
| 6 |
解答: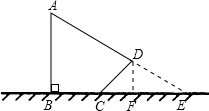 解:延长AD交地面于E,作DF⊥BE于F.
解:延长AD交地面于E,作DF⊥BE于F.
∵∠DCF=45°.CD=4.
∴CF=DF=2
.
由题意知AB⊥BC.
∴∠EDF=∠A=60°.
∴∠DEF=30°
∴EF=2
.
∴BE=BC+CF+FE=6
.
在Rt△ABE中,∠E=30°.
∴AB=BEtan30°=6
×
=6
(m).
答:电线杆AB的长为6
米.
 解:延长AD交地面于E,作DF⊥BE于F.
解:延长AD交地面于E,作DF⊥BE于F.∵∠DCF=45°.CD=4.
∴CF=DF=2
| 2 |
由题意知AB⊥BC.
∴∠EDF=∠A=60°.
∴∠DEF=30°
∴EF=2
| 6 |
∴BE=BC+CF+FE=6
| 6 |
在Rt△ABE中,∠E=30°.
∴AB=BEtan30°=6
| 6 |
| ||
| 3 |
| 2 |
答:电线杆AB的长为6
| 2 |
点评:此题主要是运用所学的解直角三角形的知识解决实际生活中的问题.作辅助线、求出BE=BC+CF+FE是解题的关键.

练习册系列答案
相关题目
 m,则电线杆AB的长度_____ m.
m,则电线杆AB的长度_____ m.
 m,则电线杆AB的长度_____ m.
m,则电线杆AB的长度_____ m.
 ,则电线杆AB的长为多少米?
,则电线杆AB的长为多少米?
 ,则电线杆AB的长为多少米?
,则电线杆AB的长为多少米?