题目内容
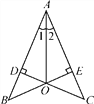
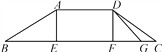
【题目】为了方便行人，市政府打算修建如图所示的过街天桥，桥面AD平行于地面BC，立柱AE⊥BC于点E，立柱DF⊥BC于点F，若AB＝5
米，tanB＝
，∠C＝30°.
(1)求桥面AD与地面BC之间的距离．
(2)因受地形限制，决定对该天桥进行改建，使CD斜面的坡度变陡，将其30°坡角改为40°，改建后斜面为DG，试计算此次改建节省路面宽度CG大约应是多少？(结果精确到0.1米，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，
≈1.732)
【答案】 (1)桥面AD与地面BC之间的距离为5米;(2) CG≈2.7米.
【解析】试题分析：(1)在Rt△ABE中,根据tanB＝
得到
,从而有
,据此即可求出AE的长;
(2)判断出四边形AEFD是矩形,在Rt△DCF中,利用三角函数解答.
解：(1)在Rt△ABE中，tanB＝
＝
，∴设AE＝x，BE＝2x，则AB＝
＝
x＝5，∴x＝5，即桥面AD与地面BC之间的距离为5米 (2)∵AE⊥BC，DF⊥BC，∴AE∥DF，∠AEF＝90°，又∵AD∥BC，∴四边形AEFD是矩形，∴DF＝AE＝5米，在Rt△DCF中，CF＝≈8.66米，在Rt△DGF中， GF＝
≈5.95(米)，改建节省所占路面的宽度为CG＝CF－GF＝8.66－5.95≈2.7(米)
练习册系列答案
相关题目
