题目内容
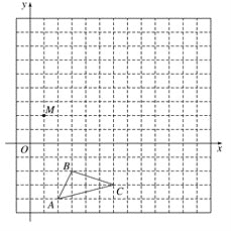
【题目】在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2，－4)，B(3，－2)，C(6，－3)．
(1)画出△ABC关于x轴对称的△A1B1C1；
(2)以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2∶1.
(3)求出A2B2、C2三点的坐标．
【答案】(1)见解析;(2)见解析;(3) A2(3,6)；B2(5,2)；C2(11,4).
【解析】
（1）直接利用关于x轴对称点的性质得出对应点位置，进而得出答案；
（2）直接利用位似图形的性质得出对应点位置，进而得出答案；
（3）直接利用图形得出各点坐标即可．
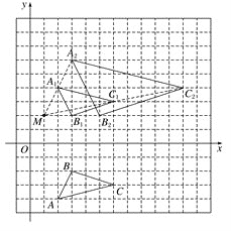
解 (1)如图所示：△A1B1C1，即为所求；
(2)如图所示：△A2B2C2，即为所求；
(3)A2、(3,6)；B2(5,2)；C2(11,4)；
故答案为：(1)见解析;(2)见解析;(3) A2(3,6)；B2(5,2)；C2(11,4).
练习册系列答案
相关题目
【题目】已知抛物线y＝ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式；
(2)已知点E(4， y)是该抛物线上的点，点E关于抛物线的对称轴对称的点为点F，求点E和点F的坐标．
