题目内容
如图,在△ABC中,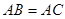 ,以AC为直径的半圆O分别交AB、BC于点D、E
,以AC为直径的半圆O分别交AB、BC于点D、E
(1)求证:点E是BC的中点
(2)若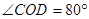 ,求∠BED的度数。
,求∠BED的度数。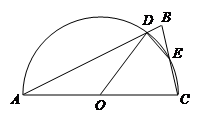
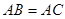 ,以AC为直径的半圆O分别交AB、BC于点D、E
,以AC为直径的半圆O分别交AB、BC于点D、E(1)求证:点E是BC的中点
(2)若
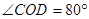 ,求∠BED的度数。
,求∠BED的度数。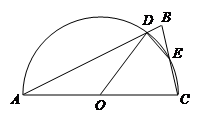
(1)见解析(2)40º
(1)证法一:连接AE, ········ 1分
∵AC为⊙O的直径,
∴∠AEC=90º,即AE⊥BC. ··········· 4分
∵AB=AC,
∴BE=CE,即点E为BC的中点.········ 6分
证法二:连接OE, ············· 1分

∵OE=OC,
∴∠C=∠OEC.
∵AB=AC,
∴∠C=∠B,
∴∠B=∠OEC,
∴OE∥AB. ················· 4分
∴ ,
,
∴EC=BE,即点E为BC的中点. ········ 6分
⑵∵∠COD=80º,
∴∠DAC=40º . ··············· 8分
∵∠DAC+∠DEC=180º,∠BED+∠DEC=180º,
∴∠BED=∠DAC=40º. 11分
(1)连接AE,根据等腰三角形的性质易证
⑵根据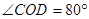 ,求得∠DAC,利用角之间的等量代换求得∠BED的度数
,求得∠DAC,利用角之间的等量代换求得∠BED的度数
∵AC为⊙O的直径,
∴∠AEC=90º,即AE⊥BC. ··········· 4分
∵AB=AC,
∴BE=CE,即点E为BC的中点.········ 6分
证法二:连接OE, ············· 1分

∵OE=OC,
∴∠C=∠OEC.
∵AB=AC,
∴∠C=∠B,
∴∠B=∠OEC,
∴OE∥AB. ················· 4分
∴
 ,
,∴EC=BE,即点E为BC的中点. ········ 6分
⑵∵∠COD=80º,
∴∠DAC=40º . ··············· 8分
∵∠DAC+∠DEC=180º,∠BED+∠DEC=180º,
∴∠BED=∠DAC=40º. 11分
(1)连接AE,根据等腰三角形的性质易证
⑵根据
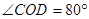 ,求得∠DAC,利用角之间的等量代换求得∠BED的度数
,求得∠DAC,利用角之间的等量代换求得∠BED的度数
练习册系列答案
相关题目
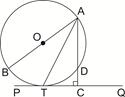
 ,求⊙O的半径。
,求⊙O的半径。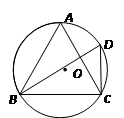
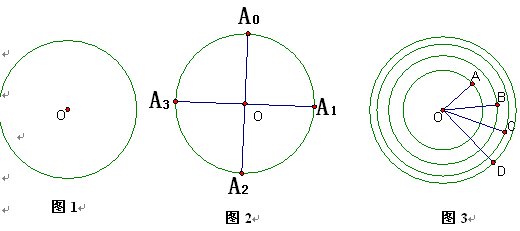
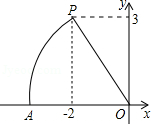
 ▲ ;
▲ ;
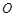 ,⊙
,⊙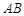 切⊙P于点
切⊙P于点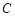 ,且
,且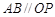 .若阴影部分的面积为
.若阴影部分的面积为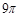 ,则弦
,则弦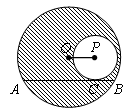
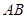 是⊙O的直径,点
是⊙O的直径,点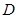 在
在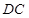 切⊙O于
切⊙O于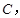 若
若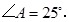 则
则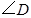 等于( )
等于( )