Question

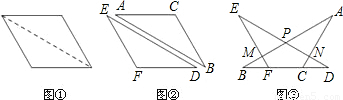
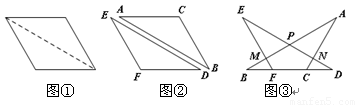
如图①，将一个内角为120°的菱形纸片沿较长对角线剪开，得到图②的两张全等的三角形纸片．将这两张三角形纸片摆放成图③的形式．点B、F、C、D在同一条直线上，AB分别交DE、EF于点P、M，AC交DE于点N．

    （1）求证：△APN≌△EPM．

（2）连接CP，试确定△CPN的形状，并说明理由．

（3）当P为AB的中点时，求△APN与△DCN的面积比．

 

Answer 1

【答案】

（1）证明见解析（2）直角三角形，理由见解析（3）△APN与△DCN的面积比为3:1

【解析】（1）由菱形性质得∠A=∠B=∠D=∠E，   ∴PB=PD． ………………1分

∵AB=DE，∴PA=PE．………………………………………………………2分

∵∠EPM=∠APN，

∴△APN≌△EPM．………………………………………………………3分

 （2）∵∠ACB=∠DFE=120°，AC=BC=DF=FE，

∴∠D=∠A=∠B=30°．∴∠ACD=60°．………………………5分

∴∠CNP=90°

∴△CPN是直角三角形…………………………………………………………6分

（3）∵CA=CB，P为AB中点，∴∠ACP=60° ……………………………………7分

    在Rt△CPN中，∴PN:CN=tan60°=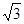:1．………………………………8分

∵∠D=∠A，∠APN=∠DNC，  ∴△ANP∽△DNC．

∴．

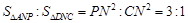即△APN与△DCN的面积比为3:1．……………………………………………9分

（1）我们可以利用菱形的性质及全等三角形的判定方法AAS判定△APN≌△EPM．

（2）求出∠D、∠ACD的度数，从而得出∠CNP=90°，从而得出△CPN是直角三角形；

（3）要求△APN与△DCN的面积比，我们可以根据菱形的性质及已知，得到PN：CN=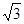，根据相似三角形的判定，得到△ANP∽△DNC，即△APN与△DCN的面积比为3：1．